Технология решения задач по алгоритму
на классическое определение вероятности

2. Алгоритм решения задач на основные теоремы вероятностей

Теорема 1
Технология решения задач по алгоритму

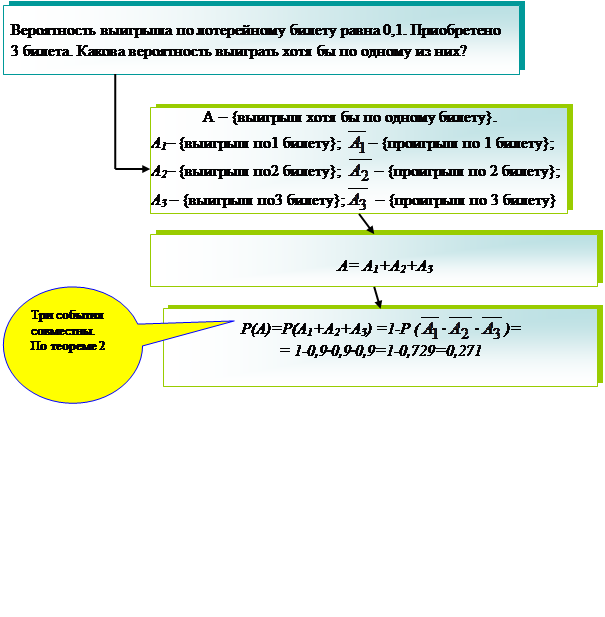
Теорема 2
Технология решения задач по алгоритму
 |
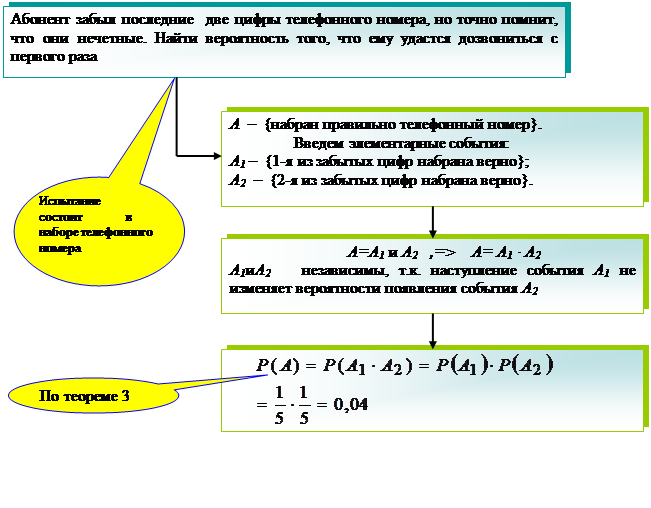
Теорема 3
Технология решения задач по алгоритму
Теорема 4
Технология решения задач по алгоритму

 Задания для самостоятельного выполнения студентами:
Задания для самостоятельного выполнения студентами:
| Вариант - 1 | Вариант - 2 |
| 1. В коллекции 200 монет, из которых 25 монет XVIII века. Какова вероятность того, что наудачу выбранная монета датирована XVIII веком ? | 1. В группе 6 юношей и 18 девушек. По жребию разыгрывается один билет в театр. Какова вероятность того, что билет получит девушка ? |
| 2. Наудачу выбирают число от 1 до 42. Какова вероятность того, что это число является делителем 42? | 2.Из чисел 1, 2, …, 8 наудачу выбираем одно. Найти вероятность того, что оно кратно 3. |
| 3. В группе 25 студентов, из них 10 юношей и 15 девушек. Какова вероятность того, что из вызванных наудачу трёх студентов - все три девушки? | 3.Группа туристов из 15 юношей и 5 девушек выбирает по жребию хозяйственную команду в составе 4-х человек. Какова вероятность того, что в составе этой команды окажутся 2 юноши и 2 девушки ? |
| 4. В лотерее 1000 билетов. На 20 из них вещевой выигрыш, на 10 – денежный. Найти вероятность выигрыша на один купленный билет. | 4. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными? |
| 5.Ученик дважды извлекает по одному билету из 34. Какова вероятность того, что он сдаст экзамен, если им подготовлено 30 билетов и в первый раз вынут неудачный билет? | 5.В двух коробках лежат карандаши одинаковой величины и формы, но разного цвета. В первой коробке 4 красных и 6 черных, а во второй 3 красных, 5 синих и 2 черных. Из обеих коробок вынимается наугад по одному карандашу. Какова вероятность того, что оба карандаша окажутся красными? |
| 6.На карточках написаны буквы «К», «А», «Р», «Т», «О», «Ч», «К», «А». Карточки перемешивают и кладут в порядке их вытаскивания. Какова вероятность того, что получится слово «КАРТОЧКА» ? | 6. На карточках написаны буквы «К», «А», «Р», «Т», «О», «Ч», «К», «А». Карточки перемешивают и кладут в порядке их вытаскивания. Какова вероятность того, что получится слово «КАРТА» ? |
| Вариант - 3 | Вариант -4 |
| 1. В коробке находится 13 белых, 9 синих и 8 красных шаров. Из коробки извлекают один шар. Какова вероятность того, что извлеченный шар окажется: а) белым; б) красным? | 1. Набирая номер телефона, вы забыли последнюю цифру и набрали ее наугад. Какова вероятность того, что набрана нужная цифра? |
| 2. Даны числа от 1 до 30 включительно. Какова вероятность того, что наудачу выбранное целое число является делителем числа 30 ? | 2. Из 35 экзаменационных билетов, занумерованных с помощью целых чисел от 1 до 35, наудачу извлекается один. Какова вероятность того, что номер вытянутого билета есть число, кратное трем ? |
| 3. В группе 25 студентов, из них 10 юношей и 15 девушек. Какова вероятность того, что из вызванных наудачу трёх студентов - первые два юноши и одна девушка ? | 3. Среди 100 колес 5 нестандартных. Для контроля выбираются 7 колес. Найти вероятность того, что среди них ровно 3 будет нестандартных. |
| 4. 20 билетов студент знает полностью, в 10 билетах он не знает по одному из 2-х вопросов; 7 билетов он не знает вообще. Считается, что студент получит положительную оценку, когда ответит хотя бы на один из двух вопросов в билете. Какова вероятность того, что студент получит положительную оценку? | 4.Один брат выучил 12 билетов из 25, другой – 15. Какова вероятность, что экзамен сдаст хотя бы один брат? |
| 5. Готовясь к вступительному экзамену по математике, абитуриент должен подготовить 20 вопросов по элементам математического анализа и 25 по геометрии. Однако он успел подготовить только 15 вопросов по элементам математического анализа и 20 по геометрии. Билет содержит 3 вопроса, 2 из которых по элементам математического анализа и 1 по геометрии. Какова вероятность, что студент сдаст экзамен на отлично (отвечает на все три вопроса)? | 5.Экзаменационный билет содержит 3 вопроса. Вероятности того, что студент ответит на первый и второй вопросы одинаковы и равны 0,9; на третий -–0,8. Найти вероятность того, что студент ответит на все вопросы. |
| 6. На каждой из шести карточек написаны буквы А, Б, И, Р, Ж. После тщательного перемешивания берут по одной карточке и кладут последовательно рядом. Найти вероятность того, что получится слово «БИРЖА». | 6. Карточки, обозначенные буквами К, Л, М, Т, О, О, О наудачу расположили в ряд. Найти вероятность того, что получится слово «МОЛОТОК». |
Выполненную и правильно оформленную работу предоставить преподавателю.








