Тема: «Вычисление предела функции в точке и на бесконечности. Два замечательных предела».
Практическое занятие № 1
Тема: «Вычисление предела функции в точке и на бесконечности. Два замечательных предела».
Цель: 1.Сформировать навык вычисления пределов функции в точке и на бесконечности; применять формулы двух замечательных пределов.
2. Способствовать развитию навыков самостоятельного применения знаний при вычислении пределов функции.
3. Способствовать привитию сознательного приобретения новых знаний по теме.
Теоретические сведения к практической работе:
Число А называют пределом функцииf(x) при 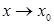 (и пишут
(и пишут 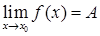 ), если для любого
), если для любого 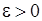 найдется число
найдется число 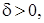 зависящее от , такое, что для всех
зависящее от , такое, что для всех 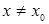 , удовлетворяющих условию
, удовлетворяющих условию 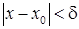 , выполняется неравенство
, выполняется неравенство 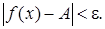
Теоремы о пределах:
1. 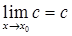 (c=const).
(c=const).
2. Если 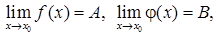 то:
то:
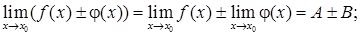
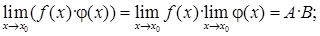
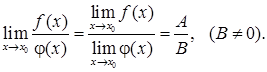
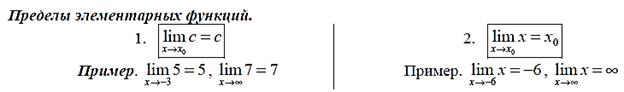
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем.
Число А называется пределом функции f( x)при х→∞, если для любого как угодно малого положительного числа ε, найдется зависящее от этого ε большое положительное число К, такое, что для всех значений аргумента, больших по величине этого числа К, значения функции отличаются по величине от указанного числа А меньше, чем на ε:
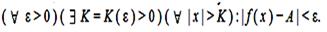

Пример. Вычислить предел 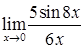
Решение 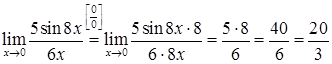
Второй замечательный предел
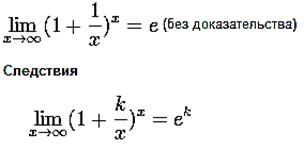
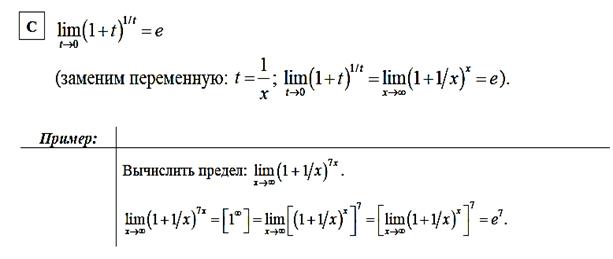
Методические указания к выполнению заданий:
Указание для задания № 1: В случае получения неопределенности воспользуйтесь алгоритмом

А) разложить числитель и знаменатель на множители, используя формулы сокращенного умножения:
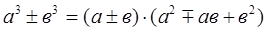
Б) разложить на множители и числитель и знаменатель по формуле ах2+bx+c=a(x-x1)(x-x2), где х1, х2 – корни уравнения.
В) домножить числитель и знаменатель на выражение сопряженное знаменателю, например:
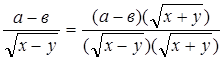
Указание для задания № 2: В случае получения неопределенности воспользуйтесь алгоритмом

В процессе вычисления пределов функций могут встретиться разные случаи. Например: 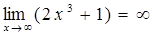 ;
; 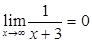
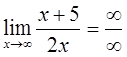 - это неопределенность вида
- это неопределенность вида 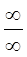 .
.
Правило: при раскрытии неопределенности вида 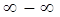 нужно числитель и знаменатель одновременно умножить на сопряженное выражение и тем самым свести к определенности вида
нужно числитель и знаменатель одновременно умножить на сопряженное выражение и тем самым свести к определенности вида 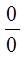 или
или 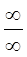 .
.
 ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ СТУДЕНТАМИ:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ СТУДЕНТАМИ:
| Вариант - 1 | Вариант - 2 |
| 1. Найти пределы функций в точке: | |
1) 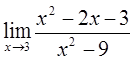 2)
2) 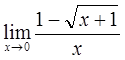 3)
3) 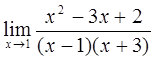 4)
4) 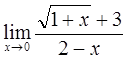 5)
5) 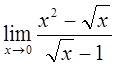 6)
6) 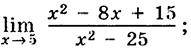
| 1) 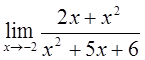 2)
2) 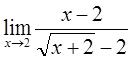 3)
3) 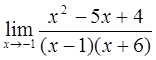 4)
4) 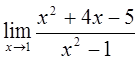 5)
5) 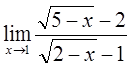 6)
6) 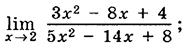
|
| 2. Найти пределы функций: | |
1) 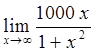 2)
2) 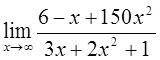 3)
3) 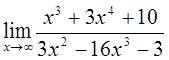 4)
4) 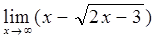 5)
5) 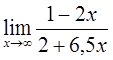 6)
6) 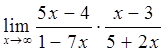 7)
7) 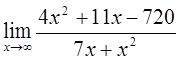 8)
8) 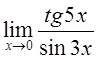 9)
9) 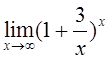 10)
10) 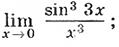
| 1) 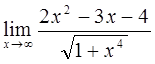 2)
2) 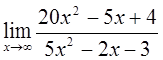 3)
3) 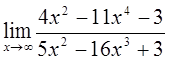 4)
4) 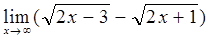 5)
5) 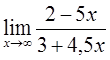 6)
6) 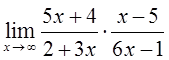 7)
7) 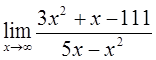 8)
8) 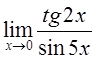 9)
9) 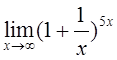 10)
10) 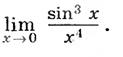
|
| Вариант - 3 | Вариант - 4 |
| 1.Найти пределы функций в точке: | |
1) 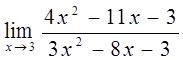 2)
2) 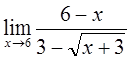 3)
3) 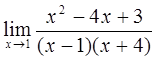 4)
4) 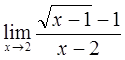 5)
5) 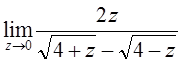 6)
6) 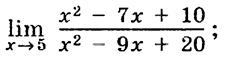
| 1) 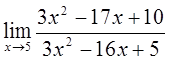 3)
3) 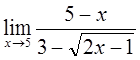 3)
3) 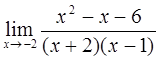 4)
4) 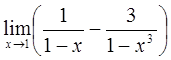 5)
5) 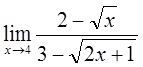 6)
6) 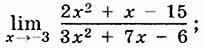
|
| 2. Найти пределы функций: | |
1) 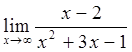 2)
2) 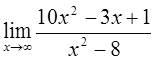 3)
3) 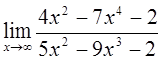 4)
4) 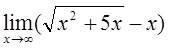 5)
5) 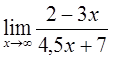 6)
6) 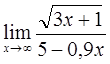 7)
7) 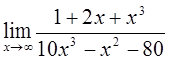 8)
8) 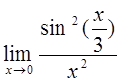 9)
9) 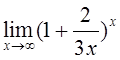 10)
10) 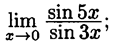
| 1) 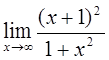 2)
2) 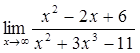 3)
3) 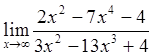 4)
4) 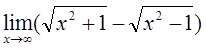 5)
5) 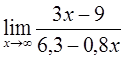 6)
6) 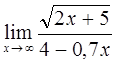 7)
7) 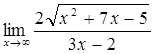 8)
8) 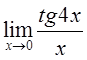 9)
9) 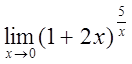 10)
10) 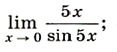
|
| Вариант - 5 | Вариант - 6 |
| 1. Найти пределы функций в точке: | |
1) 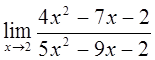 2)
2) 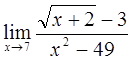 3)
3) 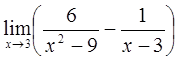 4)
4) 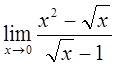 5)
5) 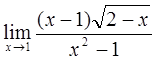 6)
6) 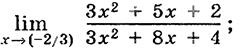
| 1) 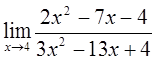 2)
2) 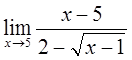 3)
3) 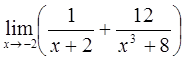 4)
4) 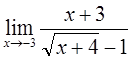 5)
5) 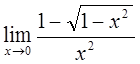 6)
6) 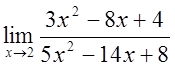
|
| 2. Найти пределы функций: | |
1) 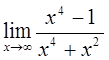 2)
2) 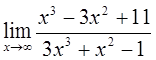 3)
3) 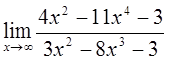 4)
4) 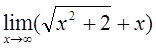 5)
5) 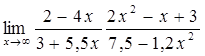 6)
6) 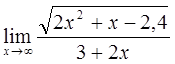 7)
7) 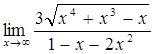 8)
8) 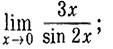 9)
9) 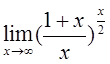 10)
10) 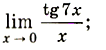
| 1) 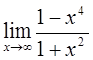 2)
2) 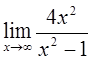 3)
3) 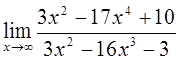 4)
4) 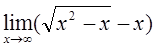 5)
5) 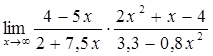 6)
6) 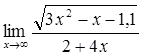 7)
7) 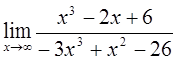 8)
8) 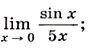 9)
9) 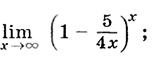 10)
10) 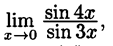
|
Выполненную и правильно оформленную работу предоставить преподавателю.








