Пусть – выборочный вектор n–наблюдений СВ Х, где . В качестве оценки для m возьмем . Предположим, что известна. Рассмотрим статистику

Дата: 2025-06-02; Просмотры: 19

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

.

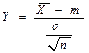Статистика .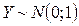

По таблице нормального распределения найдем квантил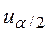и и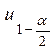

.

.

.

.

.

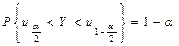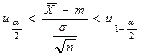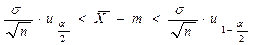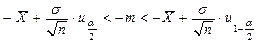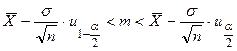Учитывая, что 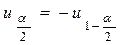получаем

.

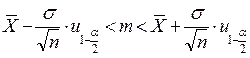ДИСПЕРСИЯ НЕИЗВЕСТНА

Пусть 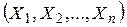– выборочный вектор n–наблюдений СВ 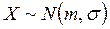. В качестве оценки для m возьмем 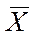. Если дисперсия генеральной совокупности неизвестна, то по выборке определяем статистику 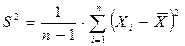. Доверительный интервал для m в этом случае находится с помощью статистики .

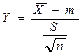В литературе по статистике показано, что Y имеет распределение Стьюдента с n–1 степенью свободы .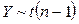

По заданной доверительной вероятности 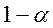, используя таблицы распределения Стьюдента с n–1 степенью свободы, находим .

.

.

.

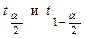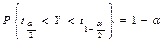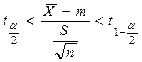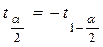
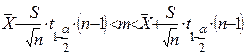Доверит.инт.для разности средних

Если дов.инт для m1-m2 содержит в себе 0, то различие 2х совокупн.незначимо и вызвано случайной изменчивостью величин и ошибкой измерений.

1.есть: N(m, 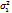) N(m, )

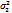n1\X1 n2\X2 (X c чертой)

σ^2 известны.

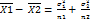и статитика Y= 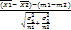~N(0,1)

рассуждая так же,как и для дов.инт для среднего с ИЗВЕСТНОЙ дисперсией:

(

2.Если Дисперсия НЕИЗВЕСТНА,то можно считать,что = =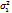

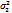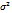
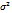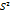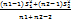= = S₁²-несмещ.оц дисп. определенная по выборке n1; S₂²-несмещ.оц дисп. определенная по выб. n2

S²несмещ оц.дисперсии σ²

использ стат Y= 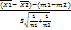~T(n1+n2-2)-степенями свободы,получ довер инт:

(

23.Проверка стат.гипотез. Классиф. Критерий. Стат.крит. Ур-нь значимости. Крит.обл. Ошибки 1 и 2 рода.

Пусть Х – наблюдаемая СВ. Она может быть дискретной, а может и непрерывной.

Статич.гипотеза Н-предположение относительно параметров или вида распределения СВ Х.

-простая –однозначно определ.распр СВ Х

-сложная

-параметрич-распр Х известно,но необходд.проверить предполож. о значениях парам-в распредел.

Проверяемая гипотеза -нулевая гип.-Н₀. Обязательно на ряду с Н₀ рассматривают одну из альтернативных гипотез Н₁.

При этом имеются различные ситуации для Н₁.

; ; ; .

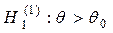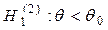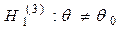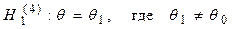Выбор альтернативной гипотезы Н₁ определяется конкретной формулировкой задачи

Критерий-правило,по кот.проверяют гипотезу

Так как решение принимается на основе выборки наблюдений СВ Х, то необходимо выбрать подходящую статистику, которую мы будем называть статистикой Z критерия К.Замечание.При проверке простой параметрической гипотезы Н₀: q = q ₀ в качестве статистики критерия выбирают ту же статистику, что и для оценки параметра q, т.е.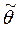

Основной принцип при проверке статистической гипотезы: Маловероятные события считаются невозможными, а события, имеющие большую вероятность, считаются достоверными. Реализация этого принципа на практике. Перед анализом выборки фиксируется некоторая малая вероятность a, называемая уровнем значимости. Пусть V множества значений статистики Z, V_K – подмножество множества значений статистики Z (V_K £ V). Это такое подмножество, что при условии истинности гипотезы Н₀, имеем вероятность того, что P { Z Î V_k ï H ₀ }= a . Обозначим через z_в – выборочное значение статистики Z, которое вычитается по конкретной выборке. Критерии К формулируется следующим образом.

Отклонить гипотезу Н₀, если z _в Î V_k. Отклонить гипотезу Н₀, если z _в Î V \ V_k. Уровень значимости a определяет размер критической области, а ее положение зависит от альтернативной гипотезы Н₁.

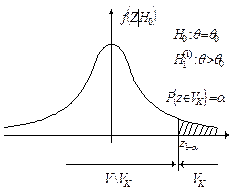
Z _{1– a} –квантиль распределения Z при условии, что верна гипотеза Н₀.

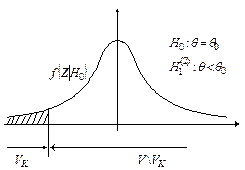
Z _a – квантиль распределения Z при условии, что верна гипотеза Н₀.

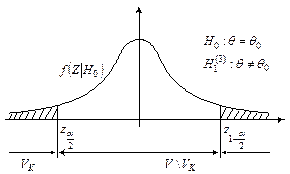
Проверку параметрической гипотезы при помощи критерия значимости можно разбить на следующие этапы:1)сформулировать Н₀ и Н₁;2)назначить a;3)выбрать статистику Z для проверки Н₀;4)определить выборочное распределение Z при условии, что верна Н₀;5)определить V_K (она зависит от Н₁);6)получить выборку и вычислить z_b ;7)принять статистическое решение: z _в Î V_k – отклонить Н₀;

z _в Î V \ V_k – принять Н₀.

Ошибка 1ого рода:

если Но отклонена,но она верна. Вероятность P { Z Î V_k ï H ₀ }= a ..-вер-ть попадания статистики Z в крит. область Vk,при усл что Но верна=

Ошибка 2ого рода:

гип. Но принимается, но верна гипотеза Н1(приняли неверную гипотезу)

Вероятность ошибки второго рода при условии, что гипотеза Н₁ – простая, P { Z Î V\ V_k ï H ₁ }= b .

Проверка гипотез с использованием критерия значимости может быть проведена на основе доверительных интервалов. При этом одностороннему критерию значимости будет соответствовать односторонний доверительный интервал, а двустороннему критерию значимости будет соответствовать, двусторонний доверительный интервал. Гипотеза Н₀ – принимается, если значение q ₀ накрывается доверительным интервалом, иначе отклоняется.

24.Проверка гипотез о равенстве дисперсий и средних.

4)так как выборка получена из нормально распределенной генеральной совокупности, выборочное среднее также имеет нормальное распределение с дисперсией 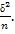При условии, что верна гипотеза Н₀, мат. ожидание этого распределения равно 10. Нормированная статистика 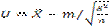имеет нормальное распределение N (0,1).

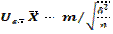
25. Регрессионный анализ. Оценки параметров линейной регрессии методом наименьших квадратов.

Зависимая переменная Y. Факторы, влияющие на Y – независимые переменные х₁, х₂, х_k. Y=f(x₁,х₂, х₃,х₄) + ε. Случайная ошибка – ε.

Уравнение множественной регрессии: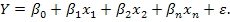

β – параметры. Коэффициент корреляции 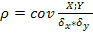. Ковариации: 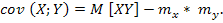Если X и Y независимы, cov (X;Y)=0, обратное не верно. Коэффициент ковариации показывает степень линейной зависимости между X и Y. Если коэффициент ковариации равен 0, то зависимости нет.

Числовые характеристики двух случайных величин:

1) M [X + Y] = M [X]+ M[Y]

2) D [X+Y] = D [X] + D [Y] + 2 cov (X;Y)

3) D [X-Y] = D [X]+D[(-Y)]+2 cov (X;Y)= D [X] + D [Y] - 2 cov (X;Y)

4) Если X и Y независимы, то cov ( X ; Y )=0, следовательно D [ X + Y ]= D [ X ]+ D [ Y ]

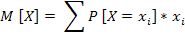
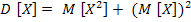
26. Анализ значимости и адекватности регрессионной модели.