Несмещенная оценка дисперсии
Пусть независимые случайные величины Xi имеют конечную дисперсию DXi = σ2. Построим оценки
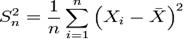— выборочная дисперсия,
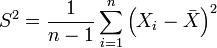— исправленная выборочная дисперсия.
Тогда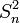 
является смещённой, а S2 несмещённой оценками параметра σ2. Смещенность можно доказать следующим образом:
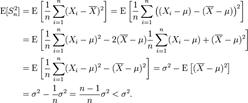
Где μ и - среднее и его оценка соответственно.
20. Распр. Хи-квадрат, Стьюдента, Фишера. Их определ. Свойства. Применение при нахождении доверительных интервалов и при проверке стат.гипотез.
1. Распр. Хи-квадрат с k степенями свободы – распредел.ссуммы квадр. K независ. стандартных нормал.случ.вел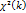 
= 
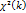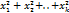. кажд Xi независ и ~N(0,1) K>0
Св-ва:
1) M( 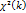)=k
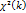D( )=2k
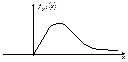
плотность распр f( )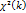
2) 
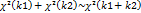
3) 
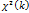~N(k,2k)
4) плотность распредел. f( 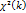) (x) = 
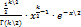,где Г(α)-гамма ф-ция, интеграл Эйлера 2ого рода. Г(α+1)= 
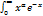dx \\\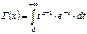 
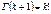
Распределение c2 определяется одним параметром числом степеней свободы. С увеличением степеней свободы распределение c2 медленно приближается к нормальному. На практике при k > 30 считают, что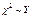 
, где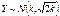 
.Для СВ, имеющей c2 распределение существуют таблицы квантилей.
формула квантилей: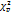 
(k)≈1\2(up+ 
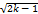)^2
2.Распр.Стьюдента c k степенями свободы
– независимая от Z СВ, которая распределена по закону c2 с k степенями свободы.
Рассмотрим СВ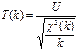 
. – обе независ.сл вел. U~N(0,1)
Св-ва
1. плотность распредел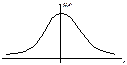 
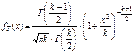
2. мат.ож и дисперсия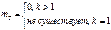 
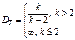
t–распределение определяется одним параметром – числом степеней свободы.
С возрастанием числа степеней свободы t–распределение асимптотически (довольно быстро) приближается к стандартному нормальному распределению с параметрами (0; 1).
Для СВ, имеющих распределение Стьюдента, имеется таблица квантилей, причем в силу четности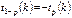 
.
3. Распр. Фишера с k 1и k 2 степенями свободы
Пусть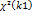 
и 
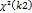- независимые случайные величины. Тогда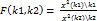 
1.Плотность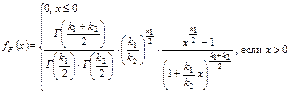 
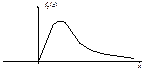
2. Мат.ож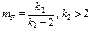 
Дисп: D[F]=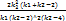 
,k2>4
3Квантили:
F–распределение определяется двумя параметрами k1 и k2 и существует таблица квантилей.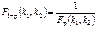 
.
Соотнош.м\д Фиш, Хи и Стьюдентом:
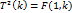
F(k,∞)=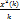 
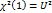
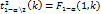t –квантиль распред.Стьюдента
____
Доверит.инт-инт.кот. покрывает неизв.параметр с заданном надежностью(исп.для бол.выборки)
инт. (θ1, θ2) содерж истинное значение θ с задан.вер-ю p=1-α . P[θ1<θ<θ2]=1-α
Стат.гип – некот.предполож. о з-не распр. СВ или о парам-е з-на,формулир.на основе выборки.
Применение:
Хи: -оценивание дисп(дов.инт),
-пров. гип.согласия,однородности,независ
Стьюдент.: -оценивание мат.ож,
-прогноз.знач и др хар-ки с пом.дов.инт
-о знач.мат ожид.
-коэф.регрессион.зависимости
Фишер:-пров.гипотез об адекватности модели в регрес.анализе
-о рав-ве дисперсий.
21. Интервал оценивание. Доверит. интервал для дисперсии. толстая тета = тета с волной,как в лекциях-оценка.а худая тета-обычная.неизв.параметр
Дов.инт для парам θ - инт. (θ1, θ2) содерж истинное значение θ с задан.вер-ю p=1-α . P[θ1<θ<θ2]=1-α
P[θ1(x1..xn)< θ < θ2(x1..xn)]=1- α – левостор. и правостор интервалы соответственно
чтоб найти дов.инт надо знать з-н распредел. статистики ϴ=ϴ (x1..xn) значение которой явл. оценкой параметра θ
Как построить доверит интервал:
есть Y=Y(ϴ θ) значения распред. Y изв и не зависят от θ
ф-ция Y неприрывна,строкго монотонна
1-α-заданная доверит.вер-ть
квантили распределения Y: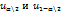 
порядков α\2 и 1- α\2
тогда верно нер-во
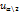< Y(ϴ θ) < 
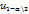. Реш относит θ и найдем θ1 и θ2 – границы дов.инт θ
Довер.инт. для дисперсии
Доверительный интервал для оценки дисперсии при неизвестном МО нормально распределенной генеральной совокупности. Пусть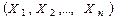 
– выборочный вектор n–наблюдений СВ 
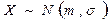. В этом случае в качестве оценки дисперсии 
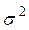используют 
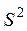=1\(n-1) 
.
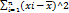В литературе по математической статистике доказано, что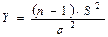 
имеет распределение 
.
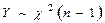По таблице распределения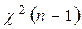 
определяются квантил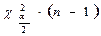и 
и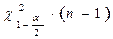 
.
.
.
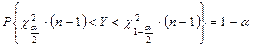
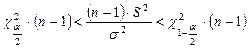
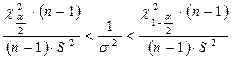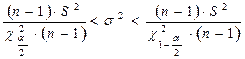При известном Мат.ож:
σ^2=S02=1\n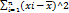
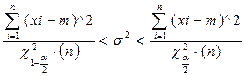
22.Доверит. интервал для среднего и разности средних
Д.инт. для среднего
ДИСПЕРСИЯ ИЗВЕСТНА