Математическое ожидание

Дата: 2025-06-02; Просмотры: 21

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

y=φ(x)

1. Пусть X- дискрет случ. вел, тогда y_n= φ(x_n)

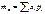
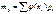
2.Пусть X –непрер. Случ. вел

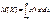
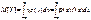
Для вычисления числовых характеристик неслучайной ф-ции случайной величины не надо знать закона распределения зависящей от X случайной величины Y, а достаточно знать закон распределения случайного аргумента X.

19. Функции нескольких случайных величин. Вычисление мат ожиданий и дисперсий для суммы случайных величин.

1. Математическое ожидание

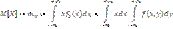
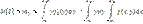
2. Дисперсия

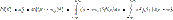
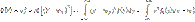
Св-ва мат. ожидания и дисперсии:

1. M[X+Y] = M[X] + M[Y]

2. M[X*Y] = M[X] * M[Y]

3. D[X+Y] = D[X] + D[Y]

3. Коэффициент ковариации

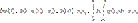
Св-ва мат. ожидания и дисперсии:

1. Если X и Y независимы, то Cov(X,Y) = 0 (обратное неверно!)

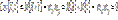
2. Cov(aX,bY) = ab*Cov(X,Y), где a и b – константы

3. Cov(X,Y)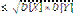

4. Коэффициент корреляции

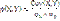
Св-ва мат. ожидания и дисперсии:

1. |ρ(X,Y)| ≤ 1, этот результат следует из свойства 3 для ковариации случайных величин X и Y.

2. Если Х и Y – независимые случайные величины, то ρ(X,Y) = 0 (по свойству 1 для ковариации)

3. Если X и Y связаны линейной функциональной зависимостью: Y=aX + b, где a и b – константы, а ≠ 0, то |ρ(X,Y)| = 1

20. Центральная предельная теорема. Теорема Муавра-Лапласа. Асимптотическое распределение среднего арифметического случайных величин.

Центральная предельная теорема.
Одна из формулировок: Пусть X1…Xn… - независимые и одинаково распределенные случайные величины с мат.ожиданием m и дисперсией σ². Рассмотрим величину X=X1+…+Xn, при n->∞ функция распределения случайной величины

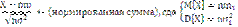
имеет нормальное распределение N(0,1) и равномерно по х сходится к функции распределения стандартного нормального закона Φ(х), где

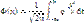
Формулировка Ляпунова Пусть X1…Xn… - независимые и одинаково распределенные случайные величины с мат.ожиданием m и дисперсией σ².

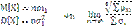
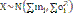
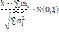
Следствия ЦПТ.

Распределение среднего арифметического случайных величин.

Пусть X1…Xn… - независимые и одинаково распределенные случайные величины с мат.ожиданием 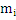и дисперсией 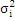. Среднее арифметическое их: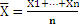

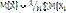]=nm/n=n

.

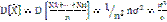При n->∞ 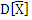-> 0. Среднее арифметическое можно представить: 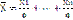, т.е. можно рассмотреть как сумму случайных величин. Тогда

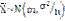– в силу центральной предельной теоремы