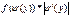Условные плотности распределения.
Распределение Y, если X принимает какое-либо значение f(Y/X)
Распределение X, если Y принимает какое-либо значение f(X/Y)
Условная ф-ция и распределения.
Распред. X, при условии Y=y
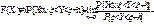
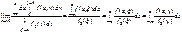
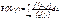
f(X/y)= 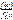 f(Y/x)=
f(Y/x)= 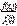
Числовые характеристики:
1. Мат ожидание:
M[X]=mx= 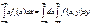
т. ожиданий. M{}
M[Y]=my т. ожиданий. M{}= 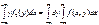 т. ожиданий. M{}
т. ожиданий. M{}
т. ожиданий. M{}
2.Дисперсия
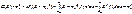
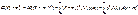
Св-ва:
M[ X + Y ]= M [ X ]+ M [ Y ]
M [ X * Y ]= M [ X ]* M [ Y ], если X и Y независимые
D [ X + Y ]]= D [ X ]+ D [ Y ], если X и Y независимые
3.Ковариация
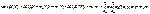
4.Коэффициент корреляции
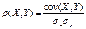 (Св-ва ковариации билет 13, св-ва корреляции билет 17.Нормальный закон на плоскости.
(Св-ва ковариации билет 13, св-ва корреляции билет 17.Нормальный закон на плоскости.
Двумерное нормальное распределение –это распределение системы двух случайных величин (X,Y) с плотностью распределения f(x,y), определяемой формулой.

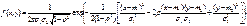 Плотность распределения случ. вел X, f1(x), вычисляется интегрированием f(x,y) по y:
Плотность распределения случ. вел X, f1(x), вычисляется интегрированием f(x,y) по y:
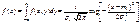 Аналогично вычисляется плотность распред случ вел Y,f2(y):
Аналогично вычисляется плотность распред случ вел Y,f2(y):
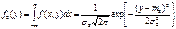 Формула (1) показывает,что в случае двумерного нормального распределения с плотностью (1) компоненты X и Y имеют нормальное распред, причем M[X]=m1, D[X]=σ12, M[Y]= m2, D[Y]=σ22
Формула (1) показывает,что в случае двумерного нормального распределения с плотностью (1) компоненты X и Y имеют нормальное распред, причем M[X]=m1, D[X]=σ12, M[Y]= m2, D[Y]=σ22
Ковариация X и Y равна
cov(X,Y)=M[(X-m1)(Y-m2)]= 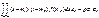 Отсюда следует,что параметр ρ в (1) есть коэффициент корреляции
Отсюда следует,что параметр ρ в (1) есть коэффициент корреляции
Св-ва:
1.Если (X,Y) имеет норм. распред.:
Каждая компоненты этого распределения также имеет нормал. распределение
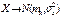
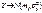
2. Если ρ=0 => f(x,y)= 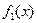 *
* 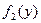 => X и Y – независимые
=> X и Y – независимые
3.Условная плотность распределения:
f(X/y) и f(Y/x) – нормальные плотности
Геометрически плотность f(x,y) двуменого нормального распределения (1) представляет «холмообразную » поверхность. Проекция вершины холма на плоскость xOy имеет координаты (m1, m2) Эта точка называется центром рассеивания.
Сечение поверхности Z=f(x,y) плоскостями , параллельными плоскости xOy, есть кривые, определяемые ур-нием:
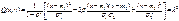 , где λ – const. Проекциями этих кривых на плоскость xOyбудут эллипсы. Т.к. плотность f(x,y) имеет на этих кривых постоянное значение, то соответствующие эллипмсы наз. эллипсами равных вероятностей
, где λ – const. Проекциями этих кривых на плоскость xOyбудут эллипсы. Т.к. плотность f(x,y) имеет на этих кривых постоянное значение, то соответствующие эллипмсы наз. эллипсами равных вероятностей
Эллипсы равных вероятностей имеют общий центр – центр рассеивания с координатами(m1, m2) и общие оси симметрии (они наз главными осями ξ и η)
18.Функции случайных величин. Вычисление мат ожиданий. Нахождение закона распределения для функции одной случайной величины, в случае дискретной и непрерывной случайной величин
Сиреневый учебник по кот ДЗ делали стр119
Функции дискретных случайных величин
Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайногвеличины Х
y=φ(x)
| X | x1 | x2 | … | xn |
| P | p1 | p2 | … | pn |
y=φ(x)
| | |||||||||||||||
Пример:
| x | -2 | -1 | 0 | 1 | 2 |
| P | 0.1 | 0.15 | 0.3 | 0.05 | 0.4 |
y=x3
| y | -8 | -1 | 0 | 1 | 8 |
| P | 0.1 | 0.15 | 0.3 | 0.05 | 0.4 |
x→y
| y | 0 | 1 | 4 |
| P | 0.3 | 0.2 | 0.5 |
y=x2
Функции непрерывных случайных величинаний. M {}
y=φ(x) – непрерывная дифференцируемая монотонная ф-ция
1.Монотонно возрастает (Лекции 13 рисунок)
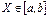
{y<Y}равносильно{x<X}
{x<X}: Fx(x)=P(x<X)= 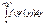 - ф-ция распределения
- ф-ция распределения
P(y<Y)=Gy(y)-ф-ция распределения
g(y)= 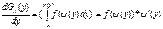
2.Монотонно убывает
X>x
P(y>Y)=Gy(y)
g(y)= 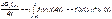
Функция плотности вероятности для функции случайной величины
y=φ(x)
g(y)=