Опр Случайные величины X1, X2,..,Xn определенные на одном дискретном вероятностном пр-ве наз. взаимно независимыми, если для любой комбинации значений xi 1 , xi 2 , .., xin. .

Дата: 2025-06-02; Просмотры: 19

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Опр Пусть случ. величины X и Yимеют конечные дисперсии. Ковариацией X и Y наз.. математическое ожидание произведения центрированных случ. величин (X-m_x) и (Y-m_y):

cov(X,Y)=M[(X-m_x)(Y-m_y)]= 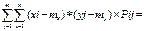M[XY]-m_xM[Y]-m_xM[X]+m_xm_y=M[XY]-m_xm_y (Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от её математического ожидания)

Св-ва cov :

1.Если X и Y независимые случ. вел, то cov(X,Y)=0, обратное же неверное, т.е. если cov(X,Y)=0, это не значит,что величины независимы.

2.cov(aX,aY)=abcov(X,Y), где a и b – константы

3.cov(X,Y)≤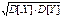

Это неравенство явл. следствием неравенства Коши-Буняковского: (M[XY])²≤M[X²]*M[Y²] (1).

Док-во нер-ва (1):

Рассмотрим очевидное неравенство M[(aX+Y)²] ≥0, где а-любое действительное число, а≠0. Преобразуем левую часть этого неравенства, используя св-ва мат. ожиданий

M[(aX+Y)²]=M[a²X²+2aXY+Y²]=a²M[X²]+2aM[XY]+M[Y²]≥0 Т. К. Полученный относительно a трехчлен принимает только неотрицательные значения, то его дискриминант будет меньше или равен нулю: 4(M[XY])²-4M[X²] *M[Y²]≤0 Отсюда следует неравенство (M[XY])²≤M[X²]*M[Y²]. Заменим X на (X-m_x), а Y на (Y-m_y), получим: (M[(X-m_x)(Y-m_y)])²≤M[(X-m_x)²]*M[(Y-m_y)²] или (cov(X,Y))²≤D[X]*D[Y]

Механическая интерпретация.

n -мерные случ. величины

(x1, x2,..,xn)- n-мерный случ. вектор

(x1, x2,..,xn)=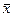

M[ 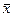]=(M[x1],…, M[xn]), т.е мат. ожидание вектора равняется вектору мат. ожиданий.

Cov(Xi;Yj)=M[(Xi-m_xi)(Yj-m_yj)], j,i=1,..,n

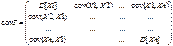
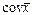-ковариационная матрица (симметрична)

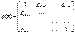
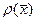-корреляционная матрица(симметрична)

D[x1+x2+x3]=D[x1]+D[x2]+D[x3]+2cov(x1,x2)+2cov(x2,x3)+2cov(x1,x3)

14.Мат. ожидание и дисперсия суммы случайных величин. Мат ожидание произведения случайных величин.

M[X]=m_x= 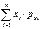M[Y]=m_y=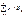

(M[X], M[Y])-центр распределения.

Пусть X и Y - случ. вел. С конечными мат. ожиданиями. Мат. ожидание их суммы равно сумме их мат. ожиданий.

M[X+Y]=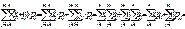

M[X]+M[Y]

Пусть X и Y- взаимно независимые случ. вел с конечными мат. ожиданиями. Мат ожидание произведения XY равно произведению их мат. ожиданий.

M[XY]= 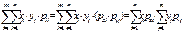=M[X]*M[Y]. Это правило распространяется на любое конечное число взаимно независимых случ. величин. Заметим, то последнее равенство для зависимых случ. величин, вообще говоря, е выполняется.

Пусть X и Y- случ. Вел с совместным распределением, задаваемым таблицей (1). Условное мат. ожидание случ. dел. X при условии, что Y принимает заданное значение

Y = yj, вычисляется по формуле: M[X/Y=yj]= 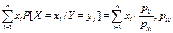>0

Дисперсия суммы случайных величин:

D[X+Y] z=X+Y =>

D[z]=M[(z-m_z)²], а m_z=m_x+m_y

D[z]= M[((X-m_x)+(Y-m_y))²]= M[(X-m_x)²]+2 M[(X-m_x)(Y-m_y)]+ M[(Y-m_y)²]=D[X]+2cov(X,Y)+D[Y]

Таким образом:

D[X±Y]=D[X]+D[Y]±2cov(X,Y)

Если X и Y независимые, то cov(X,Y)=0 => D[X±Y]=D[X]+D[Y]

Рассмотрим

D[aX±bY]=a²D[X]+b²D[Y]±2abcov(X,Y)

15.Коэффициент корреляции как характеристика статистической связи. Некоррелированность и независимость случ. величин.