2 Вероятность в дискретных пространствах элементарных событий.
1.Случайные события. Пространство элементарных событий. Алгебра событий.
Влияние случ.факторов приводит к тому,что мы постоянно получаем разл.значен-я(пр
измерении каких-либо предметов)
Случайные соб-я – это события,которые могут произойти,а могут и не произойти.
Серия экспериментов- последов-ть экспериментов,проводимых в неизменных условиях.
А-случ.соб-е
n раз повторяется эксперимент. nA –частота появления соб.А в n экспериментах.
Относит.частота hA= nA/n – статистич.опр-е(отношение числа экспериментов А к числу всех благопр.исходов)
Р(А)-вер-ть соб.А.
Такая процедура назыв.частотное определение вер-ти соб.А
Пространство элемент.соб-тий
Пример. Подбрасывание игр.кости 1 раз.
w1-выпала «1», w2- выпала «2»... w6-выпала «6»
Соб.А –выпад.четного числа очков. А={ w2; w4; w6 }
Соб.В-вып.числа очков кратных 3. В={ w3; w6 }
Множество W всех элемент.исходов данного эксперимента назыв.
пространством элементарных событий. W={ w1; w2 ... }
Операции над случ.событиями:
диаграмма Эйлер-Венна
А) событие A
Б) Суммой событий А и В назыв.соб. А+В,состоящее из элемент.соб, принадлежащ.хотя бы одному из соб.А или В.
В) Произведением событий А и B назыв.соб. АВ,сост.из элемент.соб-й,принадлеж.одновременно А и В.
Г) Разностью соб.А иВ назыв.соб-е А-В,сост.из элем.соб-й,принадлежащих А и не принадлеж.В.
Д) Соб.Ā=w/А назыв. противоположным событию A(или дополн.к соб.А)
Е) Несовместимые события (если они не могут произойти одноременно), если АВ=Æ
Ж) События образуют полную группу, если хотя бы одно из них обязательно происходит в результате испытания.
З) Если из наступления соб.А следует наступл.В,т.е соб.В есть следствие А,то это записыв.так: АÌВ.
Алгебра событий:
Система F подмножеств W,удовлетворяющая условиям:
1)WÎF; 2) из того,что А,ВÎF,следует,что А+ВÎF, ABÎF, Ā,B(с черточкой)ÎF называется алгеброй событий.
Т. о., алгебра F-это система подмножеств W,котор.замкнута относ-но конечного числа опер-й слож-я, умн-я и доп-я.
Если усл-е 2) выполн.для счетного числа соб-й,то алгебра F называется s-алгеброй(сигма-алгеброй)
2 Вероятность в дискретных пространствах элементарных событий.
Пусть W содержит либо конечное, либо счетное число элемнт.соб-й: W={w1,w2,..}
F-набор все подмножеств W. F явл. s-алгебра.
Каждому эл.исходу wi (i=1,2,..) поставим в соот-е неотриц.число P(wi)=pi, такое что å pi=1 и 0≤pi≤1.
Следствия: P(A)=å p(wi), 0≤P(A)≤1, P(W)=1, P(Æ)=0, P(Ā)=1-P(A), P(A+B)≤P(A)+P(B) или P(A+B)+P(A)+P(B)-P(AB)
Вероятностное прост-во (W,F,P) называется в этом случае дискретным.
3. Классическая схема равновероятных событий.
Если W сожержит конечное число эл.соб-й,например N соб-й, причем все эл.исходы равновозможны,т.е. p(wi)=1/N, i-1,2,..,N, то P ( A )=| A |/| W |,
где |A|-кол-во эл.исходы,составляющих множество А, а |W|- число всех эл.исходов данного эксперимента. |W|=N
Такая ф-ла назыв. классическим определением вер-ти (Если эл.исходы равновозможны, то вер-ть соб.А равна отношению числа исходов,благоприятствующих соб.А, к числу всех эл.исходов)
4 Теорема сложения и умножения вероятности.
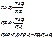P(A/B)- условная вероятность события A при условии , что соб.B произошло.
усл.вер-ть P(A/B)
усл.вер-ть P(B/A)
-теорема умножения для зависимых соб.А и В.
Если соб.А не влияет на вер-ть соб.В и наоборот,то они независимы:
P(A/B)=P(A); P(B)=P(B/A) => P(AB)+P(A)*P(B) – вер-ть произ-ния соб-й равна произ-нию вер-тей.
P(ABC)=P(AH)*P(A/H)=P(BC)*P(A/BC)=P(C)*P(B/C)*P(A/BC) (ВС обозначили за Н)
Опр-е независимости для А,В и С- соб. А,В и С назыв.независимыми в совокупности,если выполн.след усл-я:
1) Если попарно независимы P(AB)=P(A)*P(B), P(BC)=P(B)*P(C), P(AC)=P(A)*P(C).
2) P(ABC)=P(A)*P(B)*P(C)
P(A+B)=P(A)+P(B) вер-ть суммы двух несовместных событий
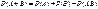- ф-ла сложения вер-тей двух совместных событий
P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC) вер-ть суммы трех несовместных соб-й
Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
5. Формула полной вероятности и формула Байеса.
Формула полной вероятности
Пусть Н1,Н2…Нk подмножества пространства эл.соб-й W, такие что:
1) Hi Hj=Æ, i≠j и I,j=1,2,…,k
2) H1+H2+…+Hk = W
В этом случае говоря,что сис-ма подмножеств Н1,Н2…Нk образует разбиение множества W. Для любого соб.А,являющего подмножеством W, верна ф-ла полной вер-ти
P(A)=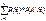 
События Hi называются гипотезами по отношению к соб.А,а вер-ти Р (Hi) трактуются как доопытные вер-ти гипотез, причем å Р (Hi)=1.
Формула Байеса
Если известно, что соб.А произошло, то априорные(после опыта) вер-ти гипотез Hi ,очевидно, должны быть пересчитаны, так как появилась доп.информация. Апостериорные вер-ти гипотез Hi ,при условии, что соб.А произошло,вычисляются по ф-ле Байеса:
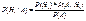,i=1,2,…,k,
где Р(А) определяется по ф-ле полной вер-ти.
истор.процесса – локальная цивилизация – общность людей, объединенных дух.традициями и проживающие на одной тер-и. Выделяет первичные, вторичные и третичные цивилизации. Свыше 20 цив-ций. Сейчас основных 8 (западно-христ, православно-христ, иудейская, исламская, индуистская, дальневосточная, буддистская, конфуцианская). 4 этапа развития: генезис, рост, упадок и дезинтеграция.
Недостатки: не принимает во внимание качественные различия хозяйственных систем в современном мире.
- теория единой цивилизации
- теория столкновения цивилизаций
6. Основные вопросы экономики и способы их решения различными экономическими системами: традиционной, административно-плановой, рыночной, смешанной. Основные черты ,преимущества и недостатки экономических систем.