2.События совместные, если возможно их одновр.наступление.
3.Событие В противоположно соб. А, если оно происх тогда и только т., когда А не происх.
4.Событие единственно возможное, если появление в р-те одного испытания одного и только одного из них явл. достоверным событием.
5.События равновозможные, если есть осн. считать, что ни одно из этих событий не явл. более возможным, чем другие.
Сов-ть событий наз. полной группой событий, если вып. 2 усл:1.обяз. насутпит одно из событий.2.наступит только одно из событий.
Операции над событиями:1. Суммой соб А и В наз. такое соб. С. , кот, происх тогда и только тогда, когда происх или соб. А. или соб В. или оба одновр.
2.Разностью А и В наз С, кот происх тогда и только тогда, когда одно из соб происх, а другое нет.
3.Произведением А и В наз С, кот происх когда происх и А и В одновр.
3.Классическое, статистическое и геометрическое опр. вероятности.
1.КЛАССИЧЕСКОЕ:
Рассм сложное событие А и предпол. , что А наступает всякий раз, когда наступают события w1w2…wn из полной группы событий. Событие w1... наз благоприятствующими для события А, если его появление влечет за собой наступление события А.
Вер-ть – это колич. мера случ. события.
Классич. опр. вводится для тех ситуаций, когда число всех исходов конечно и все исходы равновозм., т.е. наступление ни одного из исходов не меет преимущ-ва перед другими. Тогда вер-ть опр по формуле P=k/n.
Вер-ть случ. события лежит в пределах [0,1]
Недостаток классического определения не всегда устанавливается равновозможность исхода.
2СТАТИСТИЧЕСКОЕ:
Пусть некоторый опыт повторен n раз Если событие А наступило m раз то m частота события А(герб выпал 98 раз)
Отношение m/n=v(A) называется относительной частостью.
При неограниченном увеличении числа n относительные частоты устойчиво колеблются около числа p, которое называется статистической вер-тью события А
P= lim(n=∞)m/n (2)
Статистическое определение вероятности закл. в том, что за вер-ть наступления события А прин. пост вел., вокруг которой колеблются значения частостей при неогр. возрастании числа n. Статистическая вероятность устанавливается только после опыта.
3ГЕОМЕТРИЧЕСКОЕ:
Когда число вар-тов бесконечно, то прим. классич. опр. вер-ти затруднительно, поэтому прим. след подход.
Множество всех исходов рассм как Эл-ты некот плоской фигуры А. Тогда число благоприятствующих эл-тов – это некое подмножество множества А (В). В таком случае p=Sb/Sa.
5.Теорема сложения вероятностей несовместных событий и ее следствия.
Напомним, что события А и В называются несовместными, если появление события А исключает появления события В. Др словами эти события не имеют общих исходов.
Теорема Р( А+В)=Р(А)+Р(В)
Док-во:
По определению полной группы А1+А2+…+Аn=Ω
Р(Ω)=1
Сумма вероятностей противоположных событий равна 1
Р(А)+Р(А-)=1
Р(А1+А2+…+Аn)= Р(А1)+…+Р(Аn)
7. Теорема сложения вероятностей совместных событий.
Напомним, что события А и В называются совместными, если появление события А не исключает появления события В. Др словами события А и В могут наступать одновременно.
Вер-ть от суммы совместных событий является следствием из теоремы сложения вер-тей несовместных событий и находится по формуле :
P(A+B)=P(A)+P(B)-P(AB)
4.Элементы комбинаторики: размещение, перестановки и сочетания. Комбинаторика- раздел матем изучающий расп. объектов в опр. порядке и способы подсчета числа такого расположения.
При вычисл вер-ти по классич формуле необх уметь подсчитывать общее число исходов. Для такого подсчета исп след Эл-ты комбинаторики:
1. 2 основных правила:
1) правило суммы. Если объект А можно выбрать m способами, А другой объект В можно выбрать n способами то выбрать А+В (m+n) способами
2) Осн.принцип комбинаторики Если есть действие, сост из неск этапов, а каждый этап содержит опр. число вар-тов, то общ число действий равно произведению числа вар-тов на число этапов.
2.ПЕРЕСТАНОВКИ
Пусть имеется n разл. эл-тов. Тогда любой упорядоченный набор из этих эл-тов называется перестановкой. Общ. число перестановок вычисл. по формуле
Pn=n!
С повторениями:
Pm=(m1,m2,m3,…,mk)=m!/m1!m2!...mk!
3.РАЗМЕЩЕНИЯ:
Пусть имеется n разл эл-тов. Из этих n эл-тов произвольным образом выбирается k эл-тов, при этом порядок выбора эл-тов важен. Тогда общее число таких выборов опр по формуле:
Аkn=n(n-1)(n-2)x…x(n-k+1)=n!/(n-k)!
С повторениями:
Аkn =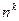 
4.СОЧЕТАНИЯ
Пусть имеется n разл эл-тов. Из этих n эл-тов произвольным образом выбирается k эл-тов, при этом порядок выбора эл-тов не важен. Тогда общее число таких выборов опр по формуле:
Ckn =n!/k!(n-k)!
С повторениями:
Ckn = Ckn+k-1
Св-ва сочетаний:
1) Cn0=Cnn=0 ( 0!=1 по соглашению)
2) Cnk=Cnn-k
3) Cn1=Cnn-1=n
8. Вероятность появления хотя бы одного из n событий, независимых в совокупности.
Пусть в р-те испытания появилось n событий независимых в совокупности, либо некоторые из них, причем вер-ти появления каждого из событий известны. Для того, чтобы найти вер-ть того, что наступит хотя бы одно из событий исп. след теорема:
Вероятность появления хотя бы одного из n событий, независимых в совокупности равна разности между единицей и произведением вероятностей противоположных событий
P(A)=1-q1q2q3…qn
Следствие: Если события A1,A2…An имеют равные вер-ти p(A)=p, то вер-ть наступления хотя бы одного из них равна:
P(A)=1-q^n
6.Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей.
События А и В наз. независимыми , если вер-ть наступления события А не зависит от того, произошло событие В или нет. (и наоборот для зависимых)
Пусть имеются два зависимых события А и В. Вероятность события А, вычисленная при условии, что событие В произошло называется усл. вер-тью события В и определяется равенством
P(А/В)=P(АВ)/P(В), где P(В)≠0
Сформ. теорему умножения вер-тей. Пусть даны зав. события А и В. Вер-ть произведения событий А и В равна произведению вер-тей одного из них на вер-ть другого, вычисл при усл, что первое событие наступило:
P(AB)= P(A)xP(B/A).
Равенство позволяет решать задачи причем оно справедливо не только для 2-х, а и для n событий. В этом случае P(A1A2…An)=P(A1)P(A2/A1)P(A3/A1A2)…P(An/A1A2…An-1)
Следствие:Для независимых событий теорема умножения примет вид: P(AB)=P(A)P(B)
9.Формула полной вероятности и формула Байеса
Рассм некот случ событие А. Оно может произойти пи выполнении одной из гипотез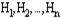 
. Указанные события образуют полную группу событий, т.е. сумма событий равна достоверному событию и произойдет только одно событие. Известны вер-ти наступления каждой из гипотез P(H1),P(H2),…,P(Hn). Также известны вер-ти наступления события А при вып каждой из гипотез (P(A/H1))… Тогда вероятность наступления события А вычисляется по формуле полной вероятности:
Р{A}=P{A|H1}P{H1}+ P{A|H2}P{H2}+…+ P{A|Hn}P{Hn}= S P{A|Hi}P{Hi}
Из формулы полной вероятности следует формула Байеса. Теорема Байеса (или формула Байеса) — одна из основных теорем теории вероятностей, которая позволяет переоценить вероятности \ гипотез после того, как становится известным результат испытания, в итоге которого произошло событие А. Ключевым словосочетанием для прим ф.Байеса явл «событие произошло». [задача про цех]
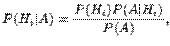
10.Повторные независимые испытания. Ф-ла Бернулли.
Имеется серия из n повторных независимых испытаний. В каждом из испытаний событие А может произойти (успех), а может не произойти (неуспех). Предполагается, что вер-ть успеха наступления события в каждом испытании постоянна и равна р. Тогда вер-ть наступл неуспеха равна q=1-р. Нас интересует событие, что в серии из n испытаний произойдет ровно k успехов. Эта вер-ть обозначается Pn(k) и вычисляя по ф. Бернулли:
Pn(k)=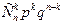 
11. Наивероятнейшее число появлений события в схеме Бернулли.
Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов (появлений события) имеет вид:
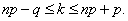
Так как ,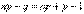 
то эти границы отличаются на 1. Поэтому k , являющееся целым числом, может принимать либо одно значение, когда np целое число (k=np) , то есть когда np+p (а отсюда и np-q) нецелое число, либо два значения, когда np-q целое число.