Свойства характеристических функций

Дата: 2025-06-02; Просмотры: 11

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Важнейшим свойством характеристической функции, сделавшим её одним из главных инструментов современной теории вероятностей, оказалось то, что при суммировании независимых случайных величин их характеристические функции перемножаются: если X и Y независимы, то для случайной величины Z=X+Y: w_Z(t)=w_X(t)×w_Y(t).

Действительно,

w_Z(t)=M(e^itZ)=M(e^it(X+Y))=M(e^itX×e^itY)=M(e^itX)×M(e^itY)=w_X(t)×w_Y(t).

Законы распределения при суммировании независимых слагаемых ведут себя гораздо сложнее (см. Л12, закон распределения суммы случайных величин).

Если Y=aX+b, то

w_Y(t)=M(e^it(aX+b))=e^itb×M(e^itaX)=e^itb×w_X(at).

Другим важным свойством характеристических функций является их простая связь с моментами.

Предполагая возможность дифференцирования под знаком математического ожидания в равенстве w(t)=Me^itX, получим:

w^(k)(t)=i^kM(X^k×e^itX).

При t=0:

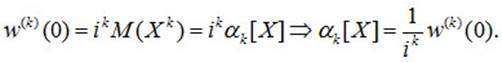
Таким образом, характеристическая функция позволяет заменить интегрирование при вычислении моментов дифференцированием.

В частности,

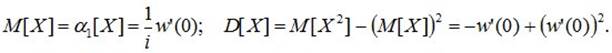
Характеристическую функцию определяют также и для n-мерной случайной величины (X₁, X₂, , ¼ , X_n):

w(t₁, t₂, , ¼ , t_n)=M(expi(t₁X₁+t₂X₂+¼+t_nX_n)).

Теория вероятностей – это мат. дисциплина, кот. изучает закономерности случайных событий и явлений. Т.о. предметом ТВ является изучение вероятностных закономерностей однор. случайных событий. Возникла в 17 веке, в связи со след. прикладными задачами:

· расчет вероятности в азартных играх,

· задача теория стрельбы (сколько раз нужно выстрелить по цели, чтобы она была поражена с заданной вер-тью)

· задача страхового дела (расчет страх. платежей, составление таблиц смертности)

· задача демографии(во всех странах, рождаемость мальчиков 0,514)

· задача теории ошибок наблюдения

Основоположники Ферма, Паскаль. Теория вероятностей развивалась в работах Лапласа, Бернули и др.(рус.-Чебышев, Марков, Ляпунов, Космогоров, Романовский и др.) Методы теории вероятностей широко применяются в разл. отраслях: теории массового обслуживания, теории стрельбы, теории автоматического управления, теории игр и др., из нее развилась мат. статистика.

2.Случайные события , их классификация. Действия над событиями

Событие– любое явление о котором имеет смысл говорить. Событие как правило рассм. при выполнении некот. комплекса усл. Изучение любого события связано с осуществлением некоторого комплекса условий которые называются опытом, экспериментом, испытанием. Результаты опыта – СОБЫТИЕ

Классиф:

1.Событие достоверное, если при выполнении комплекса условий оно произойдет (Ω/ν)

2.Событие невозможное, если при выполнении комплекса условий оно никогда не произойдет ( Пустое множество или V)

3.Событие случайное, если при выполнении комплекса условий оно может произойти/не произойти.

А:...-описание события

1.События несовместное, если появление одного из них исключает появление других в этом же испытании.