Композиция нормальных законов
Рассмотрим две независимые с.в. Х и У, подчиненные нормальным законам:
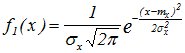и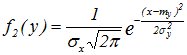 
Требуется найти композицию этих законов, т.е. найти закон распределения величины Z=X+Y.
Применяем общую формулу для композиции законов распределения:
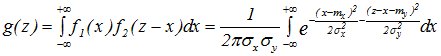. (13.3)
Раскрываем скобки в показателе степени подынтегральной функции и приводим подобные члены, получаем
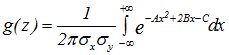, (13.4)
где
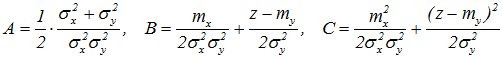
Используя интеграл Эйлера-Пуассона: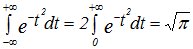 
, получаем
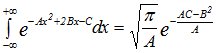Подставляем значения А, В, С в эту формулу и после преобразований, получаем:
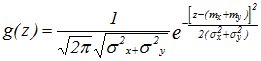- это и есть нормальный закон с центром рассеивания 
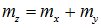и средне квадратическим отклонением
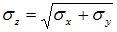
Итак, при композиции нормальных законов получается нормальный закон, причем МО и дисперсии(или квадраты с.к.о.) суммируются.
50Производящие функции.
В ряде случаев для определения важнейших числовых характеристик дискретных случайных величин может помочь аппарат производящих функций.
Пусть имеется дискретная случайная величина X, принимающая неотрицательные целочисленные значения 0, 1, …, k, … с вероятностями p0, p1, …, pk, …; pk=P{X=k}.
Производящей функцией случайной величины X называется функция вида:
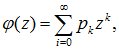
где z – произвольный параметр(0<z≤1).
Очевидно, что
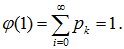
Возьмем первую производную по z от производящей функции:
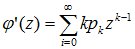
и полагаем в ней z=1:
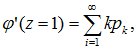
т.е. математическому ожиданию случайной величины X.
Таким образом, математическое ожидание неотрицательной целочисленной случайной величины равно первой производной ее производящей функции φ(z) при z=1.
Возьмем вторую производную функции φ(z):
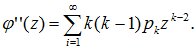
Полагая в ней z=1, получим
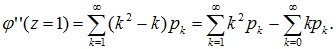
Первая сумма является вторым начальным моментом α2 случайной величины X, а вторая – ее математическое ожидание. Тогда:
,
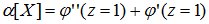т.е. второй начальный момент случайной величины равен сумме второй производной от производящей функции при z=1 плюс ее математическое ожидание.
Аналогично, берем третью производную:
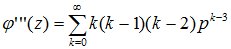
и полагая в ней z=1, получаем:
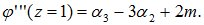
И так далее, что позволяет выразить начальные моменты более высокого порядка.
51Характеристические функции.
До сих пор мы задавали случайные величины законом распределения. Характеристическая функция - ещё один способ представления случайных величин.
Пусть X - случайная величина. Её характеристической функцией w(t) назовём математическое ожидание случайной величины eitX:
w(t)=MeitX,
где под комплексной случайной величиной eitX мы понимаем комплексное число eit X=cos(tX)+isin(tX), а
;
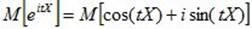независимая переменная t имеет размерность X-1.
Характеристическая функция - преобразование Фурье-Стилтьеса функции распределения:
.
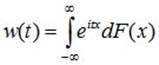В непрерывном случае w(t) - преобразование Фурье плотности вероятности:
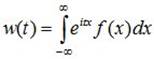
Если w(t) абсолютно интегрируема, то обратное преобразование Фурье позволяет восстановить плотность f(x) по характеристической функции:
.
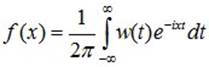В дискретном случае:
.
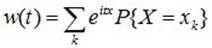Особо отметим дискретные случайные величины с целочисленными значениями, например, при xk=k:
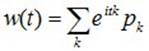
здесь w(t) - ряд Фурье в комплексной форме, вероятности pk играют роль коэффициентов Фурье и легко восстанавливаются по w(t):
.
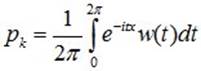В общем случае восстановление закона распределения по характеристической функции тоже возможно, но более сложно.