48Закон распределения функции непрерывной случайной величины.

Дата: 2025-06-02; Просмотры: 19

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Пусть Х – непрерывная случайная величина с известной плотностью вероятности. Алгоритм определения закона распределения СВ Y зависит от вида функции Y=j(х).

1. Рассмотрим случай монотонного возрастания функции Y=φ(x) на интервале [a,b) определения случайной величины Х (рис. 9.1).

Определим функцию распределения величины У:

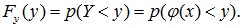
Чтобы выполнилось условие 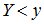, необходимо и достаточно, чтобы случайная величина Х попала на участок оси абсцисс от а до х=ψ(х), где ψ(х) – функция, обратная функции j(x).

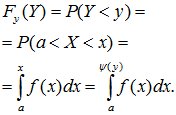
Функция распределения случайной величины Y имеет вид:

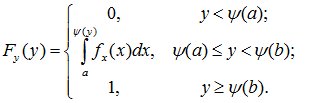
Дифференцируя интеграл по переменной у, входящей в верхний предел, получим:

.

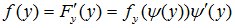2. Рассмотрим случай, когда y=φ(х) монотонно убывающая функция на интервале [a,b) определения случайной величины Х (рис. 9.2).

Функция распределения случайной величины Y определиться так:

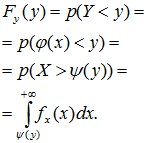
Функция распределения СВ Y=φ(х) для СВ X, распределенной в интервале [a,b], равна:

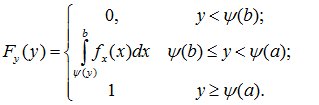
Плотность вероятностей для любого монотонного случая принимает вид:

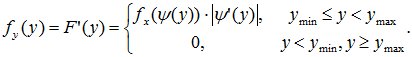(9.5)

3. Рассмотрим случай когда функция y=φ(x) на участке [a,b) возможных значений случайной величины Х не монотонна (рис. 9.3).

Число значений обратной функции ψ(y) зависит от того, какое значение Y выбрано. Событие Y<y равносильно попаданию случайной величины X в один из непересекающихся отрезков, отмеченных жирной линией на рис.9.3, где соответствующая часть кривой y-φ(X) лежит ниже прямой у. Попадания точки Х в эти отрезки – события несовместные; по правилу сложения вероятностей

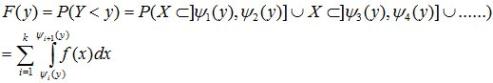(9.6)

Плотность вероятностей случайной величины Y равна

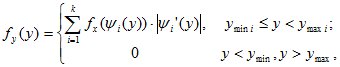(9.7)

где: k – интервалов монотонности функции φ(x);

y_min , y_max – соответственно минимальное и максимальное значение случайной величины Y;

y_mini , y_maxi – соответственно минимальное и максимальное значение случайной величины Y на i-ом интервале монотонности.

49Закон распределения суммы случайных величин. Композиция законов распределения.

Одна из важнейших для практики частной задачи, а именно – нахождение закона распределения суммы двух случайных величин.

Пусть имеется система СВ (X,Y) с плотностью распределения f(x,y). Рассмотрим сумму СВ X и Y Z=X+Y и найдем закон распределения случайной величины Z. Для этого построим линию на плоскости ХОУ линию Z=X+Y. Она делит плоскость на две части Z>X+Y и Z<X+Y. Согласно определению функции распределения:

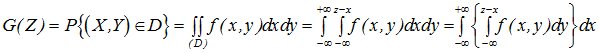
Дифференцируем это выражение по переменной Z, входящей в верхний предел внутреннего интеграла, получим

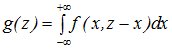(13.1)

Это – общая формула для определения плотности распределения суммы двух случайных величин. Т.к. задача симметрична, то :

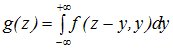. (13.2)

Особое практическое значение имеет случай, когда складываемые СВ (X,Y) независимы. Тогда говорят о композиции законов распределения.

Для независимых случайных величин X и Y

f(x, y) = f_х(x)f_у(y) Þ (12.5) и (12.6) Þ Þ

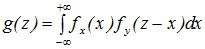и .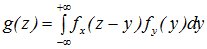

Для обозначения композиции законов применяют символическую запись: .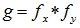

Закон распределения вероятностей называют устойчивым, если композиция таких законов есть тот же закон (отличающийся только параметрами). Нормальный закон обладает свойством устойчивости.