46Функции случайных величин. Числовые характеристики функций случайных величин. Теоремы о числовых характеристиках функций случайных величин.
Пусть некоторая случайная величина Х подвергается детерминированному преобразованию j, в результате которого получается величина У. Рассмотрим задачу определения числовых характеристик и закона распределения получаемой в результате преобразования случайной величины У.
Числовые характеристики функции случайного аргумента.
Рассмотрим случайную величину Y, зависящую функционально от случайной величины X с известным законом распределения F(x): Y=φ(X).
Если Х – дискретная случайная величина и известен ее ряд распределения имеет вид:
| Xi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
Определяем вероятности появления различных значений случайной величины У
| φ(X)i | φ(x1) | φ(x2) | … | φ(xn) |
| pi | p1 | p2 | … | pn |
Тогда математическое ожидание случайной величины Y определяется так:
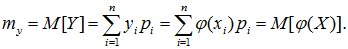 (9.1)
(9.1)
Если случайная величина X непрерывна и имеет плотность распределения f(x), то заменяя в формуле (9.1) вероятности pi элементом вероятности f(x)dx, а сумму – интегралом, получаем:

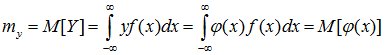 . (9.2)
. (9.2)
 Для смешанной случайной величины выражение для математического ожидания преобразуется к виду:
Для смешанной случайной величины выражение для математического ожидания преобразуется к виду:

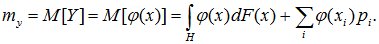 (9.3)
(9.3)
Соотношения (9.1), (9.2) и (9.3) – общее понятие математического ожидания, позволяющее вычислить математическое ожидание для неслучайных функций случайного аргумента. Например, дисперсия случайной величины Y=φ(x) определяется так:
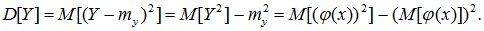
Величину M[φ(x)] рассчитываем в соответствии с (9.1)-(9.3). Для определения математического ожидания квадрата φ(х) воспользуемся следующими соотношениями:
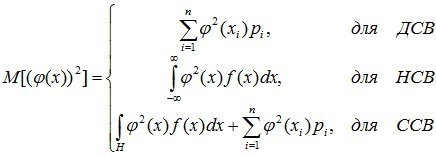 . (9.4)
. (9.4)
Таким образом, для нахождения числовых характеристик функции Y=φ(x) достаточно знать закон распределения ее аргумента.
47Закон распределения функции дискретной случайной величины.
Для дискретной случайной величины Y=φ(х) определяем вероятности появления различных значений случайной величины:
| φ(X)i | φ(x1) | φ(x2) | … | φ(xn) |
| pi | p1 | p2 | … | pn |
Преобразуем полученную таблицу в ряд распределения случайной величины Y. Для этого расположим значения Y в порядке возрастания, а для определения вероятностей p{Y=yi} будем руководствоваться следующими правилами:
· если различным возможным значениям аргумента Х соответствуют различные возможные значения Y, то P{Y=φ(xi)}=pi;
· если различным возможным значениям случайной величины Х соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений СВ Y.
Полученный таким образом ряд является рядом распределения случайной величины Y.








