44Нормальный закон распределения на плоскости.

Дата: 2025-06-02; Просмотры: 11

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Непрерывная двумерная случайная величина (X,Y) имеет нормальное распределение, если ее совместная плотность вероятности имеет вид

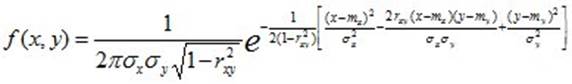
m_x – математическое ожидание случайной величины X.

m_y – математическое ожидание случайной величины Y.

σ_x – средне квадратичное отклонение СВ X.

σ_y – средне квадратичное отклонение СВY.

r_xy -- коэффициент корреляции.

Условные законы распределения СВ X и Y также являются нормальными:

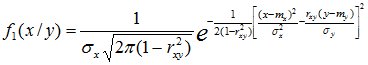; (12.2)

.

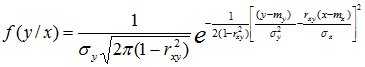Условные числовые характеристики имеют вид:

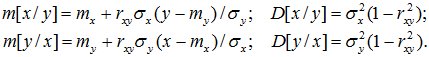(12.3)

Для системы нормально распределенных случайных величин линии регрессии m[x/y] и m[y/x] представляют собой прямые линии, т.е. регрессия линейна.

Для двумерной нормально распределенной с.в. – если составляющие некоррелированы, то они и независимы, т.е. 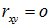Þ

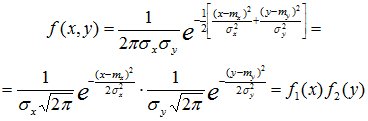(12.4)

Итак, для нормально распределенных составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.

Можно показать, что двумерная случайная величина (Х,У) распределена нормально, то Х и У связаны линейной кррреляционной зависимостью.

45Условные числовые характеристики систем случайных величин.

Пусть (Х, У) – 2-мерная СВ с известным законом распределения F(X,Y) или f(x,y). Условным математическим ожиданием компоненты Х называется математическое ожидание СВ Х, вычисленное при условии, что СВ Y приняла определенное значение Y=y и обозначается М(Х/Y). Аналогично определяется условное математическое ожидание и для СВ Y.

Используя формулы для вычисления числовых характеристик случайных величин можно вычислить и условные числовые характеристики, заменив безусловные законы распределения на условные.

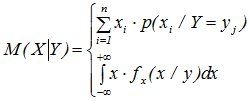и 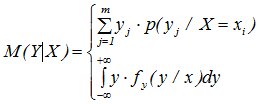(11.13)

Условное математическое ожидание СВ Y при заданном X=x: M[Y/x]=m_y/x называется регрессией Y на x; аналогично M[X/y]=m_x/y называется регрессией X на y. Графики этих зависимостей от x и y называются линиями регрессии или «кривыми регрессии».

Регрессионный анализ позволяет выявить характер связи между величинами. Представим СВ Y в виде линейной функции Х:

,

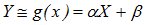где a и b - неизвестные величины.

Теорема. Линейная средняя квадратическая регрессия Y на Х имеет вид

,

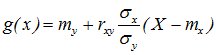здесь 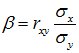- коэффициент регрессии Y на Х,

а прямую 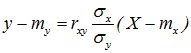- называют прямой среднеквадратической регрессии Y на Х. Аналогично можно получить прямою среднеквадратической регрессии Х на Y.

Обе прямые проходят через точку (m_x, m_y), которую называют центром совместного распределения величин Х и Y.