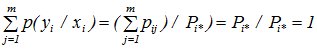38Плотность распределения системы случайных величин.

Дата: 2025-06-02; Просмотры: 20

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Двумерная величина (X,Y) является непрерывной, если ее функция распределения F(х,у) представляет собой непрерывную, дифференцируемою функцию по каждому из аргументов и существует вторая смешанная производная .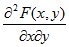

Рассмотрим на плоскости x0y прямоугольник ΔR_xy, примыкающий к точке (x,y), с размерами Δx, Δy и найдем вероятность попадания в него случайной точки (X,Y). Согласно (10.6)

.

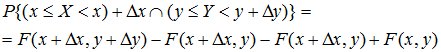Будем неограниченно уменьшать оба размера прямоугольника Δx→∞, Δy→∞ и вычисляем предел:

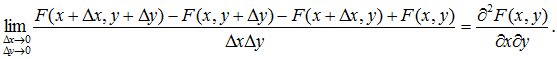
Совместной плотностью вероятности или плотностью совместного распределения называется функция

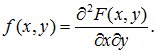(10.11)

Плотность f(x,y) обладает следующими свойствами:

1. f(x,y)≥0;

2.

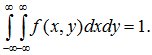
Геометрически совместная плотность f(x,y) системы двух случайных величин представляет собой некоторую поверхность распределения.

Аналогично вводится понятие элемента вероятности: .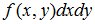

Элемент вероятности 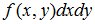с точностью до бесконечно малых величин равен вероятности попадания случайной точки (X,Y) в элементарный прямоугольник ΔR_xy, примыкающий к точке (x,y), с размерами Δx, Δy.

Аналогично тому, как было рассмотрено в случае одномерной случайной величины, определим вероятность попадания случайной точки (X,Y) в область D:

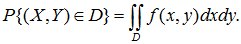(10.12)

Функция распределения системы (X,Y) через совместную плотность определяется так:

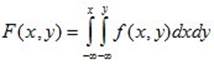. (10.13)

Совместная плотность распределения системы случайных величин (X,Y) позволяет вычислить одномерные законы распределения случайных величин X и Y :

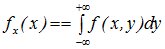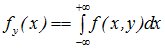; . (10.14)

Одномерные плотности распределения составляющих системы случайных величин называют маргинальными плотностями распределения.

39 Зависимые и независимые случайные величины. Условные законы

распределения системы дискретных случайных величин.

_{Величина Х не зависит от величины Y, если ее закон распределения не зависит от того, какое значение приняла величины Y.}

Для независимых величин выполняется следующие соотношения:

1. F(x,y)=p(X<x,Y<y)=p(X<x)p(Y<y)=F_X(x)F_Y(y);

2. для непрерывных случайных величин f(x, y) = f₁(x)f₂(y);

3. для дискретных случайных величин p_ij = p_i p_j , для " i, j.

Для независимых величин двумерные формы закона распределения не содержат никакой дополнительной информации кроме той, которая содержится в двух одномерных законах.

В случае зависимости величин Х и Y, переход от двух одномерных законов к совместному осуществить невозможно. Для этого необходимо знать условные законы распределения.

Условным законом распределения называется распределение одной случайной величины, найденное при условии, что другая случайная величина приняла определенное значение.

Условные ряды вероятностей для дискретных составляющих Х и Y определяются по формулам

p_i/j = P(X = x_i/Y = y_j) = p_ij/P(Y = y_j)=

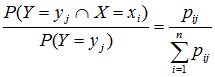, i = 1, ..., N; (10.15)

p_j/i = P(Y = y_j/X = x_i) = p_ij/P(X = x_i)=

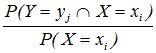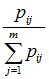= , j = 1, ..., M. (10.16)

Условное распределение может быть представлено в виде таблицы:

Заметим, что