32Равномерное распределение случайной величины.
Непрерывная случайная величина Х равномерно распределена в интервале [а; в], если ее плотность вероятности в этом интервале постоянна, т.е. если все значения в этом интервале равновероятны:
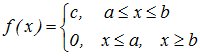 (8.1)
(8.1)
Значение постоянной с определяется из условия нормировки:
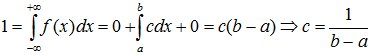 . (8.2)
. (8.2)
Функция распределения:
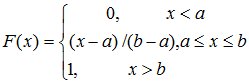 , (8.3)
, (8.3)
Числовые характеристики равномерно распределенной случайной величины определяются так:
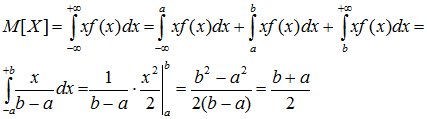 (8.4)
(8.4)
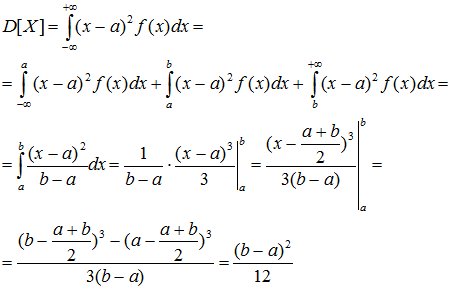 (8.5)
(8.5)
Среднее квадратичное отклонение равномерного распределения равно
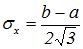 (8.6)
(8.6)
Равномерное распределение случайной величины полностью определяется двумя параметрами: a и b – интервалом, на котором определена случайная величина.
При необходимости можно определить параметры a и b равномерного распределения по известным значениям математического ожидания mX и дисперсии DX случайной величины. Для этого составляется система уравнений следующего вида:
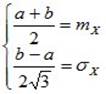 , (8.7)
, (8.7)
из которой определяются искомые параметры.
Вероятность попадания равномерно распределенной случайной величины в интервал [α,β) определяется так:
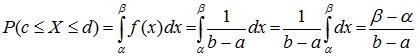 , где
, где 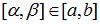
33Нормальное распределение случайной величины.
П.31
34Системы случайных величин.
Системоой случайнвх величин (случайным вектором, многомерной случайной величиной) называется любая упорядоченная совокупность случайных величин Х ={X1, …, Xn}.
Случайные величины{X1, …, Xn}, входящие в систему могут быть как непрерывными, так и дискретными. Для наглядности рассмотрения пользуются геометрической интерпретацией; так систему двух случайных величин {X,Y} можно представить случайной точкой на плоскости с координатами X и Y, или случайным вектором, направленным из начала координат в точку (X,Y).
Свойства случайных величин не исчерпываются свойствами отдельных величин, входящих в систему и необходимы средства для описания характеристик систем случайных величин.
35Системы дискретных случайных величин. Матрица распределения.
Двухмерная случайная величина (Х,У) является дискретной, если множества значений ее компонент X={x1, …, xn} и Y={y1, …, ym} представляют собой счетные множества.
Для описания вероятностных характеристик таких величин используется двухмерная функция распределения и матрица вероятности, которая содержит значения компоненты X ={x1,x2,.. xn}, Y={y1,y2, … ym} и вероятности всех возможных пар значений
pij = P(X =xi , Y = yj ) ,i=1..n , j=1..m.
Матрица распределения системы двух случайных величин записывается в виде:
| y1 | y2 | … | yj | … | ym | |
| x1 | p11 | p12 | … | p1j | … | p1m |
| x2 | p21 | p22 | … | p2j | … | p2m |
| … | … | … | … | … | … | … |
| xi | pi1 | pi2 | … | pij | … | pim |
| … | … | … | … | … | … | … |
| xn | pn1 | pn2 | … | pnj | … | pnm |
Сумма всех вероятностей pij, стоящих в матрице распределения вероятностей равна единице как сумма вероятностей полной группы событий:
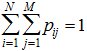 . (10.7)
. (10.7)
Зная матрицу распределения системы двух дискретных случайных величин (X,Y), можно найти закон распределения отдельных случайных величин, входящих в систему:
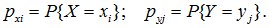
Представим событие (X=xi) как сумму несовместных событий:
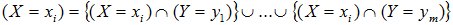 ,
,
По правилу сложения вероятностей
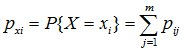 , (10.8)
, (10.8)
аналогично
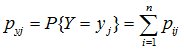 . (10.9)
. (10.9)








