29Простейший поток событий.
Физические условия возникновения распределения.
Рассмотрим временную ось, на которой будем отмечать моменты возникновения случайных событий (например, отказы компонентов в сложном техническом устройстве, заявки на обслуживание).
Поток случайных событий называется стационарным, если число событий, приходящихся на интервал t в общем случае не зависит от расположения этого участка на временной оси и определяется только его длительностью, т.е. среднее число событий в единице времени (l) (интенсивность потока) постоянно.
Поток случайных событий называется ординарным, если вероятность попадания в некоторый участок Dt двух и более случайных событий пренебрежимо мала по сравнению с вероятностью попадания на него одного события.
В потоке отсутствует последействие, если вероятность попадания событий на участок t не зависит от того, сколько событий попало на другие участки, не пересекающиеся с данным.
Поток случайных событий называется простейшим, или Пуассоновским, если он является стационарным, ординарным и без последействия. 
Для Пуассоновского потока число событий поступивших в течение интервала t является дискретной случайной величиной с распределением Пуассона с параметром α = tl
30Экспоненциальное распределение случайной величины.
Непрерывная случайная величина Х, принимающая только положительные значения имеет показательное (или экспоненциальное) распределение, если
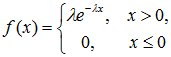, (8.8)
Положительная величина l называется параметром показательного распределения и полностью определяет его.
Определим функцию распределения случайной величины.
1. при t<0
,
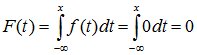2. при t≥0
.
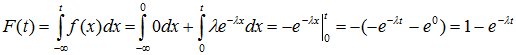Таким образом, функция распределения имеет вид:
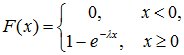(8.9)
Числовые характеристики случайной величины.
.
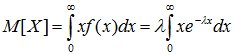Проводя интегрирование по частям и учитывая, что при x→∞ e-x стремиться к нулю быстрее, чем возрастает любая степень x , находим:
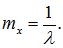(8.10)
Дисперсия случайной величины определяем по формуле:
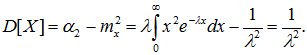(8.11)
Показательное распределение тесно связано с простейшим (стационарным пуассоновским) потоком событий. Интервал времени T между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром, равным интенсивности потока.