25Геометрическое распределение.
Дискретная случайная величина X имеет геометрическое распределение, если вероятности ее возможных значений 0,1,….,k,.. определяются так:
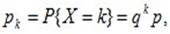
где p – параметр распределения, 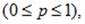 а q=1-p.
а q=1-p.
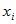
| 0 | 1 | 2 | … | k | … |
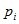
| p | 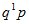
| 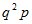
| … | 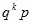
| … |
На практике геометрическое распределение появляется при следующих условиях. Пусть производится некоторый опыт, в котором некоторое событие появляется с вероятностью p. Опыты производятся последовательно, до наступления события. Случайная величина X, равная числу неудачных опытов, имеет геометрическое распределение.
Числовые характеристики геометрического распределения:
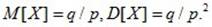
26Смещенное геометрическое распределение.
“Смещенное” геометрическое распределение получается из геометрического путем преобразования СВ X и СВ Y=X+1.
Дискретная случайная величина Y имеет смещенное геометрическое распределение если вероятности ее возможных значений 1,…,k, определяются так
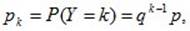
где p – параметр распределения 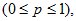 а q=1-p.
а q=1-p.
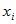
| 1 | 2 | 3 | … | k | … |
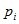
| p | 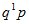
| 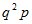
| … | 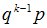
| … |
Числовые характеристики смещенного геометрического распределения определяются с использованием их свойств:
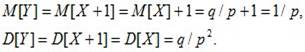
27Биномиальное распределение.
Дискретная случайная величина X имеет биноминальное распределение, если ее закон распределения описывается формулой Бернулли:
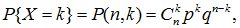
где p – параметр распределения 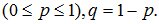
Распределение загасит от двух параметров п и р.
На практике биноминальное распределение возникает при следующих условиях. Пусть производится серия из п испытании, в каждом из которых некоторое событие появляется с вероятностью р. Случайная величина X, равная числу наступлений события в п опытах, имеет биноминальное распределение.
Числовые характеристики: М [Х] = n, D[X]= npq.
Название объясняется тем, что правую часть равенства можно рассматривать как общий член разложения Бинома Ньютона:
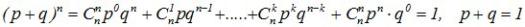 ,
,
т.е. 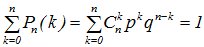 .
.
28Распределение Пуассона.
Соотношениями, описывающими биноминальное распределение, удобно пользоваться в тех случаях, если величина и достаточно мала, а р велико.
Теорема: Если, 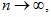 а
а 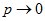 так, что
так, что 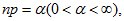 то
то
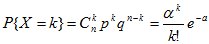
при любом k=0,1,….
Числовые характеристики: М[Х] = α, D[X] = α.
Закон Пуассона зависит от одного параметра α, смысл которого заключается в следующем: он является одновременно и математическим ожиданием и дисперсией случайной величины Х.








