Свойства математического ожидания.

Дата: 2025-06-02; Просмотры: 20

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1. Математическое ожидание неслучайной величины с равно самой величине с:

M[c] = c. (6.4)

Доказательствово: представим величину с как случайную величину, которая принимает одно и то же значение, с вероятностью р=1:

M[c]=c∙1=c.

2. При умножении СВ Х на неслучайную величину с не ту же самую величину увеличится ее математическое ожидание:

M[c×X] = c×M[X]. (6.5)

Доказательство:

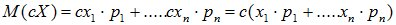
3. При прибавлении к СВ Х неслучайной величины с к ее математическому ожиданию прибавляется такая же величина:

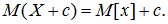(6.6)

Доказательство: следует из свойств 1 и 3.

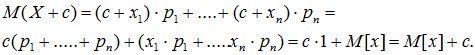
4. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

M[X+Y] = M[X]+M[Y]. (6.6)

23Дисперсия случайной величины и ее свойства.

Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной случайной величины.

Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений.

Расчетные формулы:

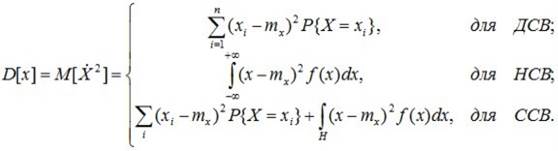(6.9)

Дисперсия может быть вычислена через второй начальный момент:

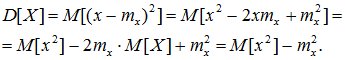(6.10)

Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания. Дисперсия СВ (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина.

Дисперсия СВ имеет размерность квадрата случайной величины. Для наглядности характеристики рассеивания пользуются величиной, размерность которой совпадает с размерностью СВ.

Средним квадратическим отклонением (СКО) СВ X называется характеристика

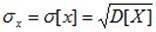. (6.11)

СКО измеряется в тех же физических единицах, что и СВ, и характеризует ширину диапазона значений СВ.

Свойства дисперсии

Дисперсия постоянной величины с равна нулю.

Доказательство: по определению дисперсии

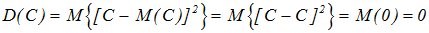
При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется.

D[X+c] = D[X].

Доказательство: по определению дисперсии

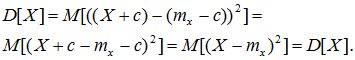(6.12)

3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с².

Доказательство: по определению дисперсии

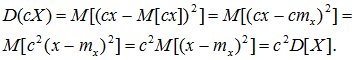. (6.13)

Для среднего квадратичного отклонения это свойство имеет вид:

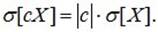(6.14)

Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М[сХ] больше, чем возможные значения Х вокруг М[X], т.е. 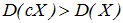. Если 0<½с½<1, то .

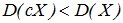Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале:

[ m - 3s; m + 3s; ].(6.15)

24Моменты высших порядков.

Понятие момента широко применяется в механике для описания распределения масс (статические моменты, моменты инерции и т.д.). Теми же приемами пользуются и в теории вероятностей. Чаще на практике применяются моменты двух видов: начальные и центральные.

Начальный момент s-го порядка СВ X есть математическое ожидание s-й степени этой случайной величины: a_s = M[X^s].

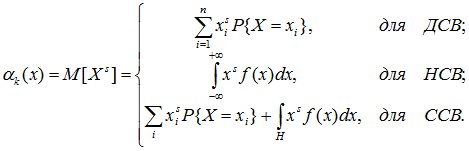(6.7)

Математическое ожидание случайной величины является начальным моментом первого порядка

Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания:

.

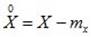Центрирование случайной величины аналогично переносу начала координат в среднюю, «центральную» точку, абсцисса которой равна математическому ожиданию случайной величины.

Центральным моментом s-го порядка СВ X есть математическое ожидание s-й степени центрированной случайной величины: m_s = M[(X-m_x) ^s].

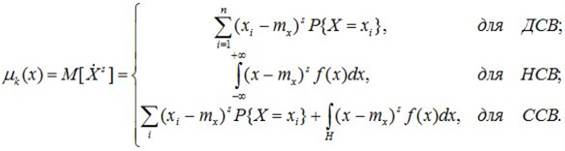(6.8)

Очевидно, что для любой случайной величины Х центральный момент первого порядка равен нулю:

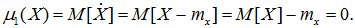
Аналогично можно получить моменты не только относительно начала координат (начальные моменты) или математического ожидания (центральные моменты), но и относительно произвольной точки а.