21Числовые характеристики случайных величин. Обобщенное понятие

Дата: 2025-06-02; Просмотры: 16
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

математического ожидания.

Законы распределения случайной величины являются исчерпывающими характеристиками. Каждый закон распределения представляет собой некоторую функцию, указание которой полностью описывает случайную величину с вероятностной точки зрения.

Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями; зачастую достаточно бывает только отдельные числовые параметры, характеризующие отдельные черты распределения; например, среднее значение или разброс случайной величины («степень случайности»). Такие числа называются числовыми характеристиками случайной величины.

Рассмотрим случайную величину Y, зависящую функционально от случайной величины X с известным законом распределения F(x): Y=φ(X).

Если Х – дискретная случайная величина и известен ее ряд распределения имеет вид:

Xi x1 x2 … xn
pi p1 p2 … pn

Определяем вероятности появления различных значений случайной величины У

 

φ(X)i φ(x1) φ(x2) … φ(xn)
pi p1 p2 … pn

 

Тогда математическое ожидание случайной величины Y определяется так:

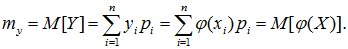(9.1)

Если случайная величина X непрерывна и имеет плотность распределения f(x), то заменяя в формуле (9.1) вероятности pi элементом вероятности f(x)dx, а сумму – интегралом, получаем:

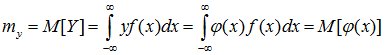. (9.2)

Для смешанной случайной величины выражение для математического ожидания преобразуется к виду:

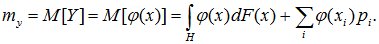(9.3)

Соотношения (9.1), (9.2) и (9.3) – общее понятие математического ожидания, позволяющее вычислить математическое ожидание для неслучайных функций случайного аргумента.

 

22Математическое ожидание случайной величины.

Математическое ожидание (МО) характеризует среднее взвешенное значение случайной величины.

Для вычисления математического ожидания для ДСВ каждое значение xi учитывается с «весом», пропорциональным вероятности этого значения.

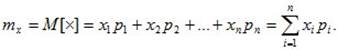(6.1)

M[X]-оператор математического ожидания;

mx -- число, полученное после вычислений по формуле.

Для НСВ заменим отдельные значения 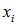непрерывно изменяющимся параметром 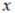, соответствующие вероятности 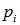- элементом вероятности 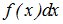, а конечную сумму – интегралом: 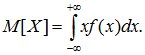(6.2)

Механическая интерпретация понятия математического ожидания: на оси абсцисс расположены точки с абсциссами 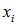, в которых сосредоточены соответственно массы р1, р2,...., причем 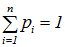. Тогда МО – абсцисса центра тяжести. Для НСВ – масса распределена непрерывно с плотностью .

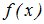Для смешанных случайных величин математическое ожидание состоит из двух слагаемых.

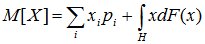, (6.3)

где сумма распространяется на все значения xi, имеющие отличные от нуля вероятности, а интеграл – на все участки оси абсцисс, где функция распределения F(x) непрерывна.

Физический смысл математического ожидания – это среднее значение случайной величины, т.е. то значение, которое может быть использовано вместо конкретного значения, принимаемого случайной величиной в приблизительных расчетах или оценках.