15Закон распределения случайной величины.

Дата: 2025-06-02; Просмотры: 18

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Законом распределения СВ называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной. (То есть, всякое соотношение, устанавливающее связь между возможными значениями СВ и их вероятностями.)

СВ будет полностью описана с вероятностной точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вероятностью обладает каждое событие. Про случайную величину мы будем говорить, что она подчинена данному закону распределения.

16Ряд распределения дискретной случайной величины.

Наиболее простую форму можно придать закону распределения дискретной случайной величины. Рядом распределения дискретной случайной величины называется таблица, в которой перечислены в порядке возрастания все возможные значения случайной величины X: x₁, x₂, …, x_n, … и вероятности этих значений p₁, p₂, …, p_n, …, где p_i=P{X=x_i} – вероятность того, что в результате опыта СВ Х примет значение x_i (i=1,2,…, n, …).

Ряд распределения записывается в виде таблицы:

Так как события {X=x1}, {X=x2}, … несовместны и образуют полную группу, то сумма всех вероятностей, стоящих в нижней строке равна единице:

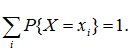(5.1)

17Функция распределения и ее свойства.

Наиболее общей формой закона распределения, пригодной для всех случайных величин (как дискретных, так и недискретных) является функция распределения.

Функцией распределения случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент функции x:

F(x)=P{X<x}.

Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки X (рис. 5.1). Из геометрической интерпретации наглядно можно вывести основные свойства функции распределения.

1. 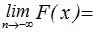F(-¥ ) = 0. (5.2)

2. 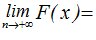F(+¥ ) = 1. (5.3)

3. F(x) – неубывающая функция своего аргумента, т.е. при x₁ < x₂

F(x₁) £ F(x₂).

Доказательство этого свойства иллюстрируется рис. 5.2.

Представим событие C={X<x₂} как сумму двух несовместных событий С=A+B, где A={X<x₁} и B={x₁£X<x₂}.

По правилу сложения вероятностей

P(C)=P(A)+P(B),

т.е. P{X<x₂}=P{X<x₁}+P{ x₁£X<x₂}, или

F(x₂)=F(x₁)+P{x₁£X<x₂}.

Но P{x₁£X<x₂}£0, следовательно, F(x₁) £ F(x₂)

4. P(α£ X < β) = F(β) - F(α), для "[α,β[ÎR. (5.4)

Доказательство этого свойства вытекает из предыдущего доказательства.

Вероятность того, что случайная величина Х в результате опыта попадет на участок от α до β (включая α) равна приращению функции распределения на этом участке.

Таким образом, функция распределения F(x)любой случайной величины есть неубывающая функция своего аргумента, значения которой заключены между 0 и 1: 0≤F(x)≤1, причем F(-∞)=0, F(+∞)=1.