2. Если A и B несовместные события, то
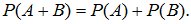(1.2)
Вторая аксиома обобщается на любое число событий: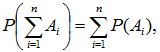 
если события Аi и Aj попарно несовместны для всех i≠j
События A1, A2, …, An называют равновозможными если
P(A1)=P(A2)= … =P(An). (1.3)
Если в каком-то опыте пространство элементарных событий Ω можно представить в виде полной группы несовместных и равновозможных событий ω1, ω2, …, ωn, то такие события называются случаями, а сам опыт сводится к схеме случаев.
Случай ωi называется благоприятным событием A, если он является элементом множества A: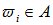 
.
Классическое определение вероятности: вероятность события определяется по формуле
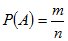, (1.4)
где n - число элементарных равновозможных исходов данного опыта;
m - число равновозможных исходов, приводящих к появлению события.
4)Аксиомы теории вероятностей.
На основе вышеизложенного сформулированы аксиомы теории вероятностей. Пусть каждому событию ставится в соответствие число, называемое вероятностью события. Вероятность события A обозначается P(A). Так как событие есть множество, то вероятность события есть функция множества. Вероятности событий удовлетворяют следующим аксиомам.
1. Вероятность любого события заключена между нулем и единицей:
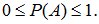(1.1)
2. Если A и B несовместные события, то
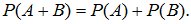(1.2)
Вторая аксиома обобщается на любое число событий: 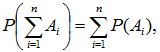если события Аi и Aj попарно несовместны для всех i≠j
З.ы. она еще следствия аксиом спрашивала
5)Геометрическое определение вероятности.
Геометрическое определение вероятности. Пусть в некоторую область случайным образом бросается точка T, причем все точки области W равноправны в отношении попадания точки T. Тогда за вероятность попадания точки T в область A принимается отношение
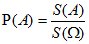, (1.5)
где S(A) и S(W) — геометрические меры (длина, площадь, объем и т.д.) областей A и W соответственно.
6)Теоремы сложения вероятностей.
Несколько событий называются несовместимыми, если появление одного из них исключает возможность появления остальных.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий
P (AÈB) =P (A) +P (B). (2.1)
Если имеется счетное множество несовместных событий A1, ... , An, то
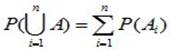. (2.2)
Из правила сложения вероятностей вытекает, что если события A1, A2, …, An несовместны и образуют полную группу, то сумма их вероятностей равна единице; т.е. если
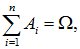AiּAj=О при i≠j, то
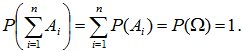(2.3)
В частности, если два события А и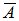 
противоположны, то они образуют полную группу несовместных событий и
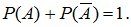(2.4)
Тогда
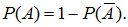(2.5)
Вероятность суммы двух совместных событий равна сумме вероятностей каждого из событий минус вероятность их совместного появления:
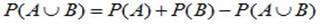. ошибка-пересечение (2.6)
7)Зависимые и независимые события. Условная вероятность события.
Событие A называется независимым от события B, если возможность наступления события A не зависит от того, произошло событие B или нет.
В противном случае события являются зависимыми. Условной вероятностью события B при наличии A называется величина
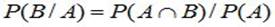(2.8)
(при этом полагается, что P(A) не равно 0).
Условную вероятность события P(B/A) можно трактовать как вероятность события B, вычисленная при условии, что событие A произошло.
Заметим, что если имеется несколько событий A1, A2, …, An, то их попарная независимость (т.е. независимость любых двух событий Ai и Aj, i≠j) еще не означает их независимости в совокупности.
8)Теоремы умножения вероятностей.
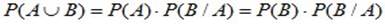ошибка-пересечение (2.9)
Вероятность произведения (пересечения, совмещения) двух событий равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого (правило умножения вероятностей).
Правило умножения вероятностей может быть обобщено на случай произвольного числа событий
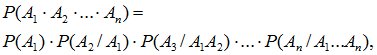(2.10)
т.е. вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого последующего события вычисляется при условии, что все предыдущие имели место.
Событие A называется независимым от события B, если его вероятность не зависит от того, произошло событие B или нет, т.е. P(B/A)=P(B).
Для независимых событий правило произведения вероятностей принимает вид:
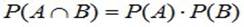.(2.11)
Несколько событий A1, A2, …, An называются независимыми, если любое из них не зависит от любой комбинации (произведения) любого числа других. Для независимых событий правило умножения принимает вид:
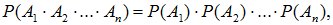(2.12)
или
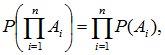(2.13)
т.е. вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий.
Заметим, что если имеется несколько событий A1, A2, …, An, то их попарная независимость (т.е. независимость любых двух событий Ai и Aj, i≠j) еще не означает их независимости в совокупности.