91. Брошены 2 игральные кости. Вероятность, что сумма очков равна 7, есть
1. Два размещения считаются различными, если они отличаются
А только порядком расположения элементов
Б) только составом элементов
В) только числом элементов
Г) или составом элементов, или их порядком
2. Два сочетания считаются различными только в том случае, если
А) у них все элементы различны
Б) отличаются порядком расположения элементов
В) отличаются двумя элементами
Г) отличаются хотя бы одним элементом
3. Перестановка 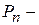 это
это
А) сочетание из n элементов по n
Б) сочетание из n элементов по 0
В) размещение из n элементов по n
Г) размещение из n элементов по 1
4. Число размещений 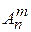 вычисляется по формуле:
вычисляется по формуле:
А) 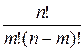
Б) 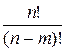
В) 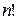
5. Число размещений 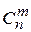 вычисляется по формуле:
вычисляется по формуле:
А) 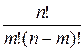
Б) 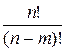
В) 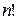
6. Число размещений 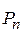 вычисляется по формуле:
вычисляется по формуле:
А) 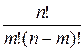
Б) 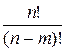
В) 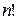
7. Случайным называется событие А, которое
А) может произойти, а может не произойти
Б) никогда не произойдет
В) обязательно произойдет
Г) произойдет только совместно с событием 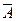
8. События А и В называются зависимыми, если
А) сумма их вероятностей обязательно равна 1
Б) вероятности событий А и В не зависят друг от друга
В) вероятность наступления одного из событий
зависит от появления или не появления другого
Г) они происходят одновременно
9. События А и В называются несовместными, если
А) вероятность наступления одного из событий
зависит от появления или не появления другого
Б) появление одного из них исключает появление другого
В) сумма их вероятностей никогда не равна 1
Г) если одновременно они могут появиться только
конечное число раз
10. Рассматривается пространство из N элементарных событий.
Событию А благоприятствуют M элементарных событий.
Классическая вероятность события А равна
А) 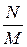
Б) 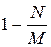
В) 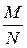
Г) 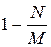
11. Произведено n испытаний. Событие А произошло m раз.
Относительная частота события А равна
А) 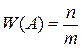
Б) 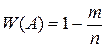
В) 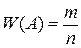
Г) 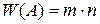
12. Вероятность 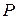 любого события принадлежит отрезку
любого события принадлежит отрезку
А) [1;2]
Б) [0;2]
В) [1;4]
Г) [0;1]
13. Сумма вероятностей событий, образующих полную группу, равна
А) 0
Б) 1/2
В) 1
Г) 4
14. Два события называются противоположными, если они
А) независимы
Б) не совместны
В) единственно возможны
Г) образуют полную группу событий
15. События образуют полную группу событий, если являются
А) независимыми
Б) единственно возможными и независимыми
В) несовместными и единственно возможными
Г) несовместными и равновозможными
16. Суммой событий А и В называется событие С,
которое происходит, если происходят:
А) только событие А
Б) только событие В
В) одно из событий А или В
Г) оба события А и В
17. Произведением событий А и В называется событие С,
которое происходит, если происходит:
А) только событие А
Б) только событие В
В) одно из событий А или В
Г) оба события А и В
18. Обязательным условием применения формулы
P(A+B)=P(A)+P(B)-P(AB)
является
А) независимость события А и В
Б) события А и В единственно возможны
В) события А и В противоположны
Г) совместность событий А и В
19. Обязательным условием применения формулы
P(A+B)=P(A)+P(B)
является
А) независимость события А и В
Б) несовместность событий А и В
В) события А и В единственно возможны
Г) совместность событий А и В
20. Вероятность P(A/B) это - …
А) вероятность события А при условии, что А и В противоположные события
Б) вероятность события А при условии, что А и В несовместные события
В) вероятность события А при условии, что событие В произошло
Г) произведение событий А и В
21. Обязательным условием применения формулы
P(AB)=P(A)P(B)
является
А) противоположность событий А и В
Б) независимость событий А и В
В) несовместность событий А и В
Г) зависимость событий А и В
22. Обязательным условием применения формулы
P(AB)=P(A)P( 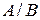 )
)
является
А) противоположность событий А и В
Б) независимость событий А и В
В) несовместность событий А и В
Г) зависимость событий А и В
23. Формула полной вероятности имеет вид:
А) 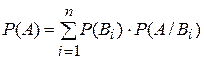 ……..
……..
Б) 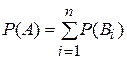
В) 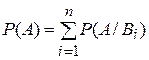
24. Случайные величины делятся на
А) переменные и постоянные
Б) четные и нечетные
В) рациональные и нерациональные
Г) дискретные и непрерывные
25. Математическое ожидание дискретной случайной
величины вычисляется по формуле
А) 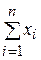
Б) 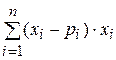
В) 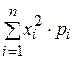
Г) 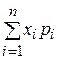
26. Математическое ожидание случайной величины (с X+Y),
где с=const, а X ,Y - независимые случайные величины,
равно:
А) cM(X)+M(Y)
Б) cM(X)-M(Y)
В) M(X)+M(Y)
Г) 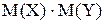
27 Математическое ожидание постоянной величины С равно
А) С
Б) 1
В) 0
Г) не определено
28. Математическое ожидание произведения двух
независимых случайных величин X и Y равно
А) M(X) + M(Y)
Б) M(X) - M(Y)
В) 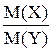
Г) 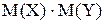
29. Дисперсия дискретной случайной величины
определяется по формуле:
А) 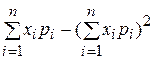 В)
В) 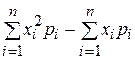
Б) 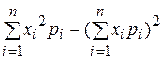 Г)
Г) 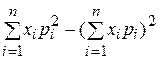
30. Дисперсия случайной величины (сX+Y),где c=const,
а X, Y - независимые случайные величины, равно
А) cD(X)+D(Y)
Б) c2D(X)+D(Y)
В) D(X)+D(Y)
Г) cD(X)-D(Y)
31. Дисперсия разности двух независимых
случайных величин X и Y равна:
А) D(X)-D(Y)
Б) 0
В) D ( X )+ D ( Y )
Г) 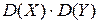
32. Дисперсия постоянной величины С равна
А) 1
Б) C
В) 0
Г) не определена
33. Математическое ожидание квадрата отклонения М(Х - М(Х))2 равно
А) D(X)
Б) 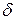 (Х)
(Х)
В) M(X)
Г) V
34. Дисперсия от математического ожидания D(M(X)) равна
А) М(Х)
Б) 0
В) Х
Г) 1
35. Среднее квадратическое отклонение 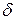 (х) случайной величины Х равно
(х) случайной величины Х равно
А) D(X)
Б) 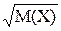
В) 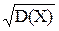
Г) M(X)
? 36. Математическое ожидание M(X) непрерывной
случайной величины X, заданной на интервале (a,b),
определяется формулой:
А) M(x)= 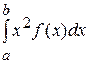 В) M(x)=
В) M(x)= 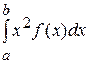
Б) M (x)= 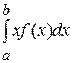 Г) M(x)=
Г) M(x)= 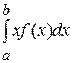
37. Дисперсия D(X) непрерывной случайной величины,
заданной на интервале (a, b), определяется формулой
А) D(X)= 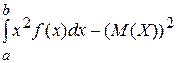 В) D(X)=
В) D(X)= 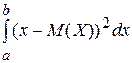
Б) D(X)= 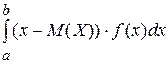 Г) D(X)=
Г) D(X)= 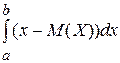
38. Графическая форма задания закона распределения
случайной величины - это
А) парабола
Б) прямая линия
В) окружность
Г) полигон
39. Табличная форма задания закона распределения
случайной величины называется
А) суммой распределения
Б) интегралом распределения
В) рядом распределения
Г) полем распределения
40. Дискретная случайная величина принимает …:
А) только множество целых значений
Б) только множество положительных значений…….тоже не уверен
В) все значения из интервала (-∞; +∞)
Г) конечное или бесконечное счетное множество значений
41. Непрерывная случайная величина принимает
А) множество целых значений
Б) множество рациональных значений
В) конечное множество значений
Г) любое значение из конечного или бесконечного интервала
42. Если X - непрерывная случайная величина,
a и b - конкретные значения, то отсюда следует, что
А) Р(а≤Х<b) ≠ Р{а<Х≤b)
Б) Р(а<Х≤b) ≠ Р(а<Х<b)
В) Р(а<Х<b) ≠ Р(а≤Х≤b)
Г ) Р ( а ≤X<b) = P(a≤X≤b) = P(a<X≤b) = P(a<X<b)
43. Если f(x) - плотность распределения, то 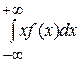 равен
равен
А) ∞
Б) -1
В) 0
Г) 1
44. Если f(x) - плотность распределения, то 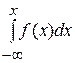 определяет
определяет
А) M(X)
Б) D(X)
В) 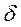 (X)
(X)
Г) F(X)
45. График плотности нормального распределения называется
А) кривой Гаусса
Б) кривой Бернулли
В) кривой Пауссона
Г) кривой Лапласа
46. Дискретная случайная величина, выражающая число появления события А в n независимых испытаниях, проводимых в равных условиях и с одинаковой вероятностью появления события в каждом испытании, называется распределенной по … :
А) нормальному закону
Б) по закону Пуассона
В) биномиальному закону
Г) по показательному закону
47. Если случайная величина имеет биномиальное распределение, n - число независимых испытаний, а p - вероятность наступления события, то математическое ожидание вычисляется по формуле
А) M(X)=n
Б) M(X)=p
В) M(X)=npq
Г) M ( X )=np
48. Если случайная величина имеет биномиальное распределение, n - число независимых испытаний, а p - вероятность наступления события, то дисперсия случайной величины вычисляется по формуле
А) D ( X )=npq
Б) D(X) = np
В) D(X) = n - p
Г) D(X) = p
49. Математическое ожидание равномерно распределенной случайной величины вычисляется по формуле
А) M(X)= 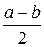
Б) M ( X )= 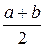
В) M(X)= 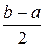
Г) M(X)=a+b
50. Дисперсия равномерно распределенной случайной величины вычисляется по формуле
А) D(X)= 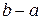
Б) D(X)= 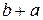
В) D ( X )= 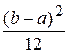
Г) D(X)= 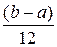
51. Вероятность попадания равномерно распределенной
случайной величины в интервал 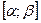
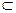 [a,b]
[a,b]
вычисляется по формуле:
А) P( 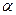 ≤X≤
≤X≤ 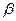 )=
)= 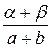
Б) P( 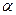 ≤X≤
≤X≤ 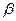 )=
)= 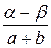
В) P( 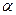 ≤X≤
≤X≤ 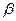 )=
)= 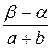
Г) P ( 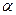 ≤ X ≤
≤ X ≤ 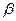 )=
)= 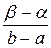
52. Плотность распределения случайной величины
с показательным распределением имеет вид:
А) f(x)= 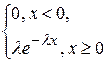 В) f(x)=
В) f(x)= 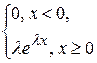
Б) f(x)= 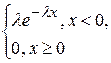 Г) f(x)=
Г) f(x)= 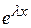
53. Функция распределения случайной величины
с показательным распределением имеет вид:
А) F(x)= 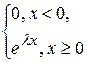 В) F(x)=
В) F(x)= 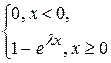
Б) F(x)= 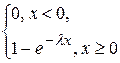 Г) F(x)=
Г) F(x)= 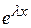
54. У показательного распределения математическое ожидание и среднее квадратическое отклонение
А) всегда различны
Б) всегда различаются на единицу
В) всегда равны
55. В точке x=a кривая Гаусса имеет
А) точку перегиба
Б) точку минимума
В) точку разрыва
Г) точку максимума
56. Точки 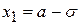 и
и 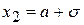 являются для кривой Гаусса
являются для кривой Гаусса
А) точками перегиба
Б) точками максимума
В) точками минимума
Г) точками разрыва
57. Функция плотности нормального распределения с математическим ожиданием a и средне – квадратическим отклонением 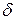 задается формулой:
задается формулой:
А) 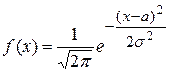 В)
В) 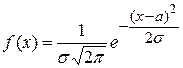
Б) 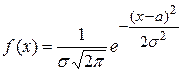 Г)
Г) 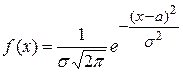
58. Параметрами нормального распределения являются:
А) математическое ожидание и среднеквадратическое отклонение
Б) функция распределения и функция плотности распределения
В) функция р(х) и Ф(х)
Г) дисперсия и среднеквадратическое отклонение
59. Функция распределения случайной величины X задается формулой:
А) 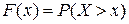
Б) 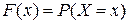
В) 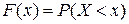
Г) 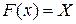
60. Вероятность появления события А m раз в n повторных независимых испытаниях при n<10 определяется
А) формулой Бернулли
Б) локальной теоремой Лапласа
В) интегральной теоремой Лапласа
Г) формулой Пуассона
61. Наивероятнейшим числом наступлений события А в n независимых испытаниях называется
А) наибольшее число наступлений события А
Б) наибольшая вероятность наступления события А
В) число наступлений события А при наибольшем числе испытаний
Г) число наступлений события А, при котором вероятность наступления события А в n независимых испытаниях наибольшая
62. Локальная теорема Лапласа позволяет вычислить
А) наивероятнейшее число наступлений события в n независимых испытаниях
Б) относительную частоту наступлений события в n независимых испытаниях
В) вероятность появления события m раз в n независимых испытаниях (n>10)
Г) вероятность отклонения числа появлений события m от числа независимых испытаний n
63. Интегральная теорема Лапласа позволяет вычислить
А) вероятность появления события A m раз в n испытаниях (n>10)
Б) вероятность появления события A в n испытаниях не менее а, но не более b раз (n>10)
В) наивероятнейшее число появлений события A в n независимых испытаниях (n>10)
Г) относительную частоту наступлений события A в n независимых испытаниях
64. В локальной теореме Лапласа 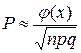 аргумент функции
аргумент функции 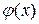 равен
равен
А) 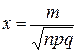 В)
В) 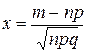
Б) 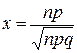 Г)
Г) 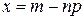
65. В интегральной формуле Лапласа 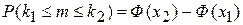 , аргумент
, аргумент 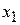 равен
равен
А) 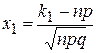
Б) 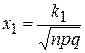
В) 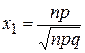
Г) 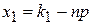
66. В интегральной формуле Лапласа 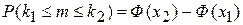 , аргумент
, аргумент 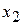 равен
равен
А) 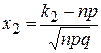
Б) 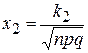
В) 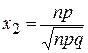
Г) 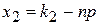
67. Формула для определения наивероятнейшего числа m0 имеет вид
А) 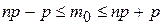
Б) 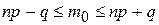
В) 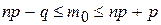
Г) 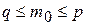
68. Надежностью оценки числовой характеристики генеральной совокупности называется
+А) вероятность попадания этой характеристики в доверительный интервал
Б) отношение предельной ошибки выборки к средней ошибке
В) доверительный интервал
Г) точность оценки
69. Доверительный интервал – это интервал, в который с надежностью 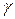 попадает
попадает
А) характеристика генеральной совокупности
Б) характеристика выборочной совокупности
В) значение изучаемого признака генеральной совокупности
Г) значение изучаемого признака выборочной совокупности
70. При повторном отборе зарегистрированные и обследованные единицы
А) вновь возвращаются в генеральную совокупность и снова могут принять участие в дальнейшем отборе
Б) в генеральную совокупность не возвращаются
В) в генеральную совокупность возвращаются, но принять участие в дальнейшем отборе не могут
Г) помечаются специальным знаком
71. При бесповторном отборе зарегистрированные и обследованные единицы
А) возвращаются в генеральную совокупность
Б) не возвращаются в генеральную совокупность
В) возвращаются в генеральную совокупность и могут принять участие в дальнейшем отборе
Г) либо возвращаются, либо не возвращаются в генеральную совокупность
72. Статистические гипотезы
А) выдвигаются о выборочных совокупностях, а проверяются по генеральным совокупностям
Б) выдвигаются о выборочных совокупностях, а проверяются тоже по выборочным совокупностям
В) выдвигаются о генеральных совокупностях, а проверяются по выборочным совокупностям
Г) выдвигаются о генеральных совокупностях, а проверяются тоже по генеральным совокупностям
73. Проверяемая гипотеза обозначается
А) Н0
Б) H2
В) H1
Г) H3
74. При статистической проверке гипотез критические точки это
А) множество точек, образующих область принятия H0
Б) множество точек, образующих область принятия H1
В) точки, разделяющие область принятия гипотезы H0 и область отвергания H0
Г) область существования H0
75. Множество всех значений критерия, при которых H0 отвергается, называется
А) областью определения
Б) областью принятия гипотезы
В) критической областью
Г) областью существования
76. Альтернативная (конкурирующая) обозначается через
А) H0
Б) H2
В) H3
Г) H1
77. Исправленная выборочная дисперсия определяется по формуле
А) 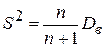 В)
В) 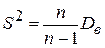
Б) 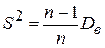 Г)
Г) 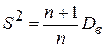
78. При статистической проверке гипотез уровнем значимости 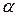 называется:
называется:
А) вероятность допустить ошибку 1 – ого рода, т.е. принять правильную нулевую гипотезу
Б) вероятность допустить ошибку 1 – ого рода, т.е. отвергнуть правильную нулевую гипотезу
В) вероятность допустить ошибку 2 – ого рода, т.е. отвергнуть правильную нулевую гипотезу
Г) вероятность допустить ошибку 2 – ого рода, т.е. принять неправильную нулевую гипотезу
79. При статистической проверке гипотез мощностью критерия называют величину 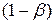 , то есть:
, то есть:
А) вероятность допустить ошибку 1 – ого рода, т.е. принять правильную нулевую гипотезу
Б) вероятность допустить ошибку 1 – ого рода, т.е. отвергнуть неправильную нулевую гипотезу
В) вероятность недопущения ошибки 2 – ого рода, т.е. отвергнуть правильную нулевую гипотезу
Г) вероятность допущения ошибку 2 – ого рода, т.е. принять неправильную нулевую гипотезу
80. Ошибка второго рода состоит в том, что
А) отвергается альтернативная гипотеза 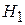 , когда на самом деле она верна
, когда на самом деле она верна
Б) отвергается нулевая гипотеза 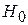 , когда на самом деле она верна
, когда на самом деле она верна
В) принимается альтернативная гипотеза 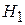 , когда на самом деле она неверна
, когда на самом деле она неверна
Г) принимается нулевая гипотеза 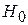 , когда на самом деле она неверна
, когда на самом деле она неверна
81. Число сочетаний 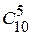 равно
равно
252
82. Число размещений 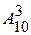 равно
равно
720
83. В отделе из 16 человек нужно выбрать начальника отдела, его заместителя и профорга. Число способов равно
3360
84. Вероятность P(A)=0,8, тогда P( 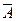 ) равна
) равна
0,2
85. На склад поступает продукция трех цехов. Доли цехов соответственно равны: 1) 45%; 2) 25%; 3) 30%. Процент брака в продукции первого цеха 4%, второго цеха 8%, третьего – 6%. Полная вероятность того, что случайно взятое на складе изделие – бракованное, равна
0,056
86. Вероятность того, что размер изделия не соответствует стандарту, равна 0,8. Вероятность того, что вес изделия не соответствует стандарту, равна 0,9. Вероятность, что изделие не стандартно, равна
0,98
87. Вероятность того, что студент Иванов сдаст сессию на «отлично», равна 0,9. Вероятность, что студент Петров сдаст сессию на «отлично», равна 0,6. Вероятность, что оба студента станут отличниками, равна
0,5 4
88. Вероятность наступления каждого из трех событий p=0,8. Вероятность наступления хотя бы одного из них равна
0,992
89. В корзине 5 красных и 8 желтых яблок. Извлекается одно яблоко и съедается. Вероятность второй раз извлечь красное яблоко, если в первый раз извлечено красное, равна
5/39
90. Осенью в речной порт Казани приходят пассажирские суда только из трех городов: Нижнего Новгорода, Москвы и Самары. Вероятность прибытия из Москвы равна 0,1, из Нижнего Новгорода – 0,6. Вероятность прибытия из Самары равна
0,3
91. Брошены 2 игральные кости. Вероятность, что сумма очков равна 7, есть
1/6
92. Если 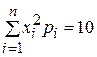 , a
, a 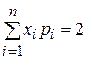 , то дисперсия случайной величины равна
, то дисперсия случайной величины равна
5
93. Случайная величина равномерно распределена на отрезке [2,6]. Ее дисперсия равна
4/3
94. Случайная величина равномерно распределена на отрезке [2,10]. Ее математическое ожидание равно
6
95. Случайная величина имеет биномиальное распределение с параметрами n=70 и p=0,3. Ее математическое ожидание равно
21
96. Случайная величина имеет биномиальное распределение с параметрами n=70 и p=0,3. Ее дисперсия равна
14,7
97. В первом ящике находятся шары с номерами 1-5 во втором – с номерами 6-10. Из каждого ящика вынули по 1 шару. Какова вероятность того, что сумма номеров вынутых шаров не меньше 7?
1
98. В урне 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули
один шар, какова вероятность того, что синий или черный?
1/2
99. Три стрелка, независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго –0,8 и для третьего – 0,95. Определить вероятность того, что все три стрелка одновременно попадут в цель.
0,57
100. В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из 3-х человек. Какова вероятность (при случайном выборе) выбрать трех мальчиков?
11/203
101. Вероятность попадания стрелком в цель 0,8, сделано 25 выстрелов, определить наивероятнейшее число попаданий.
20
102. Рабочий за смену может изготовить 130 деталей. Вероятность того, что это изделия высшего сорта 0,95. Определить наивероятнейшее число изделий высшего сорта, изготовленных рабочим.
124








