Магнитные пускатели – это электрические аппараты, объединяющие контакторы и тепловые реле. Тепловые реле обеспечивают защиту электрической цепи электродвигателей от перегрузок.
Реле – это коммутационный аппарат небольшой мощности, реагирующий на заданную физическую величину (напряжение, ток, частоту, давление). Реле предназначено для выполнения управляющих, защитных и логических операций в системах автоматического управления и защиты.
В зависимости от предназначения реле делятся на минимальные и максимальные реле (тока, напряжения), промежуточные реле, реле времени. В зависимости от принципа действия реле подразделяются на электромагнитные, тепловые, реле давления. На рис.14.2 показана конструктивная схема электромагнитного реле клапанного типа.
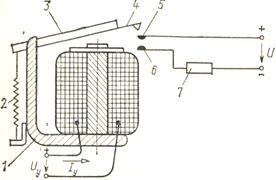
Рис.14.2. Устройство электромагнитного
реле клапанного типа
При подаче управляющего сигнала Uy на катушку реле возникает электромагнитная сила притяжения якоря 3 к ярму 1 и реле срабатывает, замыкая контакты 5 и 6 с помощью клапана 4. После срабатывания реле исполнительный механизм 7 производит требуемое действие. При обесточивании катушки реле противодействующая пружина 2 отводит якорь 3 от ярма 1 и происходит размыкание контактов.
Автоматические выключатели представляют собой сочетание теплового реле, контактора, дугогасительного устройства и механизма расцепления контактов. Они обеспечивают автоматическое отключение цепи при нарушении нормального режима работы (при перегрузках, коротких замыканиях).
15. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Электрическую цепь называют нелинейной, если она содержит нелинейные элементы, параметры R, L или С которых зависят от значений или направлений тока и напряжения.
Вольт-амперная характеристика нелинейных элементов (НЭ) (рис.15.1) отличается от прямой линии и характеризуется в каждой точке значениями статического и динамического сопротивлений.
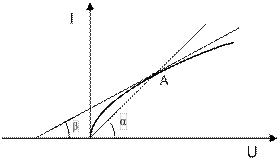
Рис.15.1. Вольт-амперная характеристика НЭ
Статическое сопротивление R ст можно определить графически, как тангенс угла наклона α между прямой, проведенной из начала координат через рассматриваемую точку А характеристики и осью абсцисс:
,
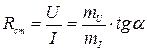где mU – масштаб напряжения,
mI – масштаб тока.
Динамическое сопротивление можно определить графически, как тангенс угла наклона β касательной к рассматриваемой точке А вольт-амперной характеристики и осью абсцисс:
.
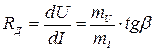Условное графическое обозначение нелинейного резистивного элемента имеет вид
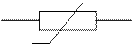
Нелинейные элементы могут быть неуправляемыми (диод, стабилитрон, варистор и др.) или управляемыми (тиристор, транзистор и др.)
Принцип действия многих электрических устройств, используемых в энергетике, радиотехнике и телевидении, основывается на свойствах нелинейных элементов.
Так, сильная зависимость сопротивления выпрямительных диодов от полярности приложенного напряжения (рис.15.2) используется для преобразования переменного напряжения в постоянное.
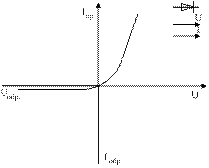
Рис.15.2. Вольт-амперная характеристика
выпрямительного диода
В стабилизаторах напряжения применяются стабилитроны – приборы, напряжение на которых в некотором диапазоне изменения тока остается практически неизменным.
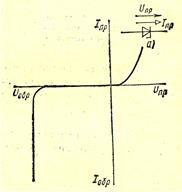
Рис.15.3.Вольт-амперная характеристика
полупроводникового стабилитрона:
Iпр, Uпр- прямой ток и напряжение,
Iобр., Uобр.- обратный ток и напряжение
У нелинейного элемента варистора существует нелинейная зависимость сопротивления от напряжения (чем напряжение больше, тем сопротивление меньше).
Расчет нелинейных цепей можно выполнить графическим методом. При последовательном соединении нелинейных элементов ток в обоих элементах будет одинаковым (точки А1 и А2 на вольт-амперных характеристиках НЭ (рис.15.4)). Проекции точек А1 и А2 на ось напряжений будут соответствовать напряжениям U1 и U2 на первом и втором НЭ. Общее напряжение в сети будет равно U1 + U2 = Uab.
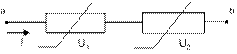
Задавая различные значения токов, можно получить соответствующие значения напряжений и построить суммарную вольт-амперную характеристику нелинейной цепи.
При параллельном соединении НЭ (рис. 15.5) напряжение на элементах будет одинаковым, что соответствует точкам В1 и В2 на вольт-амперных характеристиках. Далее находим токи I1 и I2, а затем суммарный ток I= I1 + I2, после чего строим суммарную характеристику:
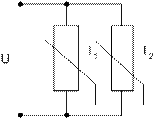
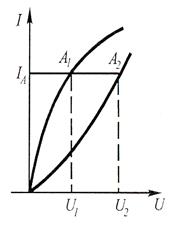
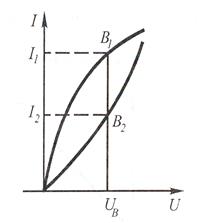
Рис.15.4. Графический метод Рис.15.5. Графический метод
расчета электрических цепей расчета электрических цепей
при последовательном соединении при параллельном соединении
нелинейных элементов нелинейных элементов
Uab=U1+U2 Iab=I1+I2
Для расчета нелинейных цепей используют также аналитический и графо-аналитический методы.
16. Переходные процессы в электрических цепях
Переход от одного режима работы цепи к другому (включение и выключение отдельных участков, подключение отдельных элементов) происходит не мгновенно, а в течение некоторого промежутка времени. Процессы, происходящие в цепи в этот период времени, называются переходными процессами. Включение и выключение элементов и участков цепи называется коммутацией.
Переходные процессы связаны с перераспределением энергий между реактивными элементами (конденсатором и катушкой индуктивности) и с необратимыми преобразованиями энергии в резистивных элементах.
Изменения энергий в электрическом поле конденсатора (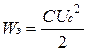 
) и в магнитном поле катушки ( 
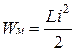) не могут происходить мгновенно. Продолжительность переходного процесса ограничена и в большинстве случаев составляет секунды или доли секунды.
Во время переходного процесса токи и напряжения могут быть в несколько раз больше, чем в установившемся режиме, и привести к аварии. Подбирая значения параметров отдельных элементов и применяя специальные схемы их включения, можно ускорить или замедлить время переходного процесса, а также ограничить скачки тока и напряжения во время переходного процесса.
Первый закон коммутации – ток в индуктивном элементе не может измениться скачком:
iL ( t - ) = iL ( t + ),
где t – момент времени, в который произошла коммутация в цепи.
Второй закон коммутации – напряжение на емкостном элементе не может измениться скачком:
uc ( t - ) = uc ( t + ).
Однако следует иметь в виду, что токи и напряжения на резистивных элементах, а также ток в емкостном элементе ic =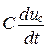 
и напряжение на индуктивном элементе 
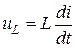могут изменяться скачком.
Переходные процессы в электрических цепях описываются системой дифференциальных уравнений, составленных по законам Кирхгофа или Ома для мгновенных значений напряжений и токов u , i (классический метод расчета).
Для простых цепей эту систему уравнений можно свести к обыкновенному линейному неоднородному уравнению, в котором в качестве искомой величины выбирают либо ток в индуктивном элементе, либо напряжение на емкостном элементе.
Общее решение линейного неоднородного дифференциального уравнения равно сумме частного решения неоднородного уравнения, в качестве которого выбирают установившийся после коммутации режим, и общего решения однородного уравнения, которое называют свободной составляющей (при отсутствии внешнего источника энергии).
Токи и напряжения, которые получаются в результате частного решения для установившегося режима (определяются параметрами источника энергии и элементов электрической цепи), называют установившимися i уст , u уст .
Токи и напряжения, получаемые в результате общего решения однородного дифференциального уравнения (правая часть равна нулю), определяются лишь параметрами элементов цепи и называются свободными i св , u св , они всегда затухают за счет потерь в цепи.
Переходные токи i пер и напряжения u пер равны сумме установившихся и свободных составляющих:
i пер = i уст + i св
u пер = u уст + u св .