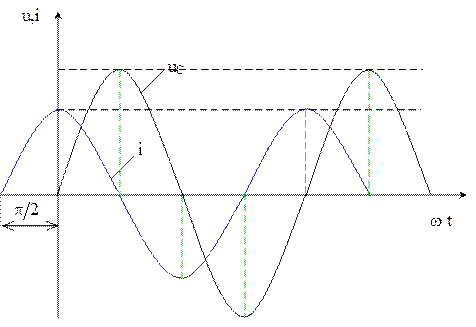
Из приведенных выражений следует, что в цепи с конденсатором ток опережает напряжение по фазе на угол p /2.
Величина 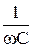 , измеряемая в единицах сопротивления и обозначаемая XC, называется емкостным сопротивлением
, измеряемая в единицах сопротивления и обозначаемая XC, называется емкостным сопротивлением
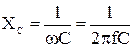 .
.
Емкостное сопротивление обратно пропорционально частоте приложенного напряжения.
Закон Ома в комплексной форме:
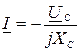 .
.
Закон Ома для действующих значений
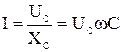 .
.
Временные диаграммы
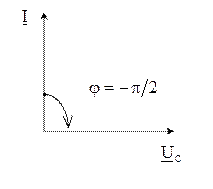
Векторная диаграмма
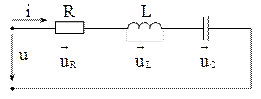
Цепь с последовательным соединением элементов R , L , C
Если к участку с последовательным соединением элементов R, L, C приложено синусоидальное напряжение 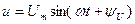 , то и ток в цепи синусоидальный
, то и ток в цепи синусоидальный 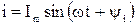 . При этом следует иметь в виду, что начальная фаза тока yi будет определяться соотношением между R, L, C.
. При этом следует иметь в виду, что начальная фаза тока yi будет определяться соотношением между R, L, C.
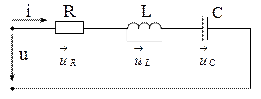
На каждом из элементов будет падать напряжение 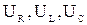 .
.
По второму закону Кирхгофа для мгновенных значений можно записать
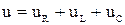 .
.
Для комплексных выражений можно записать
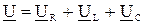 .
.
Подставив в выражение 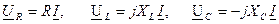 , получим закон Ома в комплексной форме:
, получим закон Ома в комплексной форме:
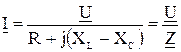 ,
,
где 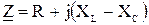 – комплексное сопротивление;
– комплексное сопротивление;
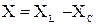 – реактивное сопротивление.
– реактивное сопротивление.
Представим комплексное сопротивление 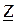 в показательной форме:
в показательной форме:
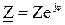 ,
,
где 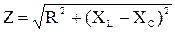 – модуль комплексного сопротивления, который называют полным сопротивлением;
– модуль комплексного сопротивления, который называют полным сопротивлением;
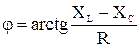 – аргумент комплексного сопротивления.
– аргумент комплексного сопротивления.
Для удобства запоминания формулы строят треугольник сопротивлений
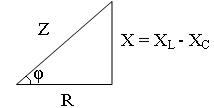
В рассматриваемой цепи знак угла сдвига фаз j между током и напряжением определяется знаком реактивного сопротивления
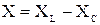 ,
,
то есть соотношением между индуктивным и емкостным сопротивлениями.
Если 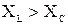 , то нагрузка в цепи имеет активно-индуктивный характер, то есть ток по фазе отстает от напряжения на угол
, то нагрузка в цепи имеет активно-индуктивный характер, то есть ток по фазе отстает от напряжения на угол 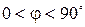 .
.
Если 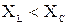 , то нагрузка имеет активно-емкостный характер, то есть ток по фазе опережает напряжение.
, то нагрузка имеет активно-емкостный характер, то есть ток по фазе опережает напряжение.
В качестве примера рассмотрим пример построения векторной диаграммы для случая, когда в цепи 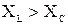 .
.
Начальную фазу тока примем равной нулю, то есть 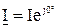 . Для напряжений по второму закону Кирхгофа можно записать
. Для напряжений по второму закону Кирхгофа можно записать
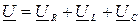 .
.
Так как 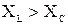 , то будет соблюдаться условие
, то будет соблюдаться условие 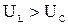 .
.
Векторная диаграмма будет иметь вид:
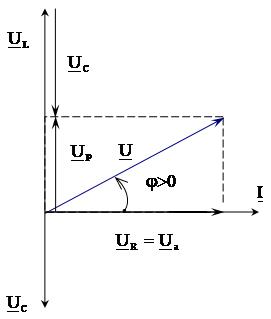
где 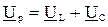 - реактивная составляющая напряжения
- реактивная составляющая напряжения 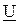 , приложенного к рассматриваемой цепи;
, приложенного к рассматриваемой цепи;
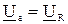 - активная составляющая напряжения
- активная составляющая напряжения 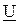 .
.
Порядок построения векторной диаграммы:
- строим вектор тока 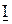 (при нулевой начальной фазе он расположен горизонтально);
(при нулевой начальной фазе он расположен горизонтально);
- строим вектор падения напряжения 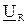 на активном сопротивлении (он совпадает по направлению с вектором тока
на активном сопротивлении (он совпадает по направлению с вектором тока 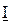 , сдвиг фаз равен нулю);
, сдвиг фаз равен нулю);
- строим вектор падения напряжения 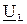 на индуктивном сопротивлении (он опережает по фазе вектор тока на 90°);
на индуктивном сопротивлении (он опережает по фазе вектор тока на 90°);
- строим вектор падения напряжения 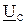 на емкостном сопротивлении (конденсатора) (он отстает по фазе от вектора тока на 90°);
на емкостном сопротивлении (конденсатора) (он отстает по фазе от вектора тока на 90°);
- складывая векторы 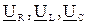 , получаем вектор общего напряжения
, получаем вектор общего напряжения 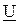 , который опережает по фазе на угол j>0 вектор тока
, который опережает по фазе на угол j>0 вектор тока 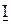 , что указывает на активно-индуктивный характер нагрузки.
, что указывает на активно-индуктивный характер нагрузки.
Мощность цепи синусоидального тока
В цепи переменного тока различают три вида мощности.
1. Активная мощность Р обусловлена наличием в цепи активного сопротивления R. В активном сопротивлении происходит необратимое преобразование электрической энергии в другие виды, например, в резисторе происходит преобразование электрической энергии в тепловую энергию
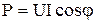 .
.
Единица измерения активной мощности – ВАТТ.
2. Реактивная мощность Q обусловлена наличием реактивных элементов (катушек и конденсаторов)
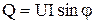 .
.
Единица измерения ВАр – ВОЛЬТ-АМПЕР реактивный (р).
На реактивных сопротивлениях ХL и ХC имеет место процесс колебания энергии от катушки индуктивности к конденсатору и наоборот; необратимых преобразований нет.
Для индуктивного элемента QL > 0, для емкостного элемента QC < 0.
При последовательном соединении L и C суммарная реактивная мощность
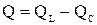 .
.
3. Кроме активной и реактивной мощностей цепь синусоидального тока характеризируется полной мощностью S. Единица измерения ВА (ВОЛЬТ – АМПЕР).
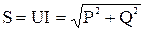
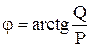 .
.
Треугольник мощностей
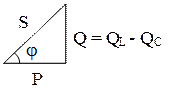
Коэффициент мощности и его экономическое значение
Коэффициентом мощности называют отношение активной (полезной) мощности к полной мощности S:
cos j = 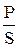 .
.
Он показывает, какая часть электрической энергии, потребляемой из сети, используется на выполнение полезной работы. При низком коэффициенте мощности машины переменного тока и трансформаторы, проектируемые на заданную полную мощность, оказываются недоиспользованными по активной мощности, что приводит к непроизводительным капитальным затратам.
Повышение коэффициента мощности приемников электрической энергии способствует уменьшению потерь энергии в электрических сетях, обмотках трансформаторов и электрических генераторов. Для повышения экономичности систем электроснабжения предприятий в настоящее время устанавливается допустимое значение реактивной мощности и нормируется значение
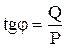 .
.
Этот показатель определяется по показаниям счетчиков активной и реактивной энергии.
Резонанс в цепях переменного тока
Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный (ХL) и емкостный (ХС) элементы, при котором угол сдвига фаз j между напряжением и током равен нулю (j=0). Различают резонанс напряжений и резонанс токов.
Резонанс напряжений возникает на участке цепи с последовательным соединением R,L,C. При этом индуктивное сопротивление равно емкостному, то есть XL = XC.
Угол сдвига фаз j определяется по формуле
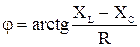 .
.
Так как при резонансе напряжений 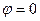 , то XL = XC или
, то XL = XC или 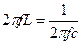 .
.
Из последнего соотношения следует, что резонанса напряжения в цепи можно достигнуть следующими способами:
- изменением индуктивности L катушки;
- изменением электрической емкости С конденсатора;
- изменением частоты тока f питающей сети.
Характерные особенности резонанса напряжений
1. Полное сопротивление Zрез цепи при резонансе равно активному сопротивлению
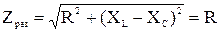 .
.
2. Резонансный ток в цепи имеет максимальное значение
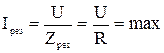 .
.
Резонансный ток может привести к перегреву элементов цепи.
Зависимость тока I от частоты f имеет вид:
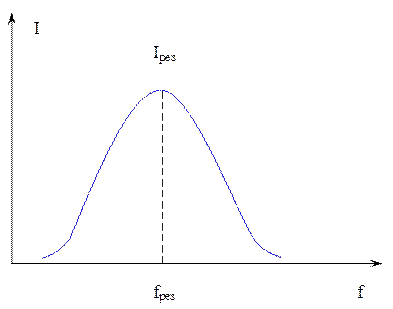
3. Напряжение на участке с активным сопротивлением R равно напряжению питания U и совпадает с ним по фазе 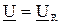 .
.
4. Активная мощность при резонансе имеет максимальное значение
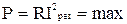 .
.
Можно предположить, что в цепи существует следующее соотношение между активным (R) и реактивными сопротивлениями ( 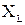 и XC):
и XC):
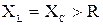 ,
,
тогда можно записать
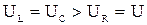 .
.
То есть напряжения на участках с реактивными элементами (UL и UC) будут больше напряжения питания U.
Свойство усиления напряжения на реактивных элементах при резонансе напряжений используется в технике.
Коэффициент усиления напряжения равен добротности Q контура
 .
.
Однако повышенное напряжение на реактивных элементах может привести к пробою электрической изоляции проводов и представлять опасность для обслуживающего персонала.
Векторная диаграмма при резонансе напряжений строится с учетом особенностей режима резонанса
j=0, 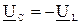 ,
, 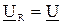
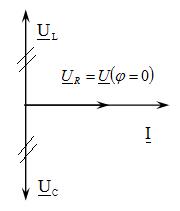
Резонанс токов
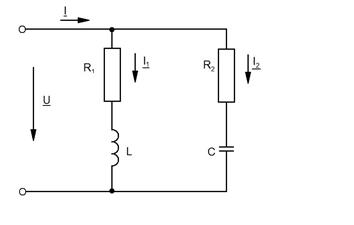



 Резонанс токов возможен в цепи с параллельным соединением двух ветвей с параметрами
Резонанс токов возможен в цепи с параллельным соединением двух ветвей с параметрами 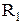 ,
, 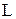 и
и 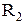 ,
, 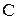 в параллельном контуре.
в параллельном контуре.


Индуктивная проводимость 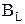 первой ветви рассматриваемой цепи определяется по формуле
первой ветви рассматриваемой цепи определяется по формуле
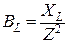 ,
,
где 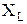 – индуктивное сопротивление катушки;
– индуктивное сопротивление катушки; 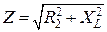 – полное сопротивление ветви.
– полное сопротивление ветви.
Емкостная проводимость 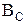 ветви с конденсатором определяется по формуле
ветви с конденсатором определяется по формуле
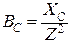 ,
,
где 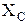 – емкостное сопротивление конденсатора;
– емкостное сопротивление конденсатора; 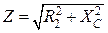 – полное сопротивление ветви.
– полное сопротивление ветви.
Угол сдвига фаз 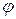 между током и напряжением при известных проводимостях ветвей параллельного контура определяется по формуле
между током и напряжением при известных проводимостях ветвей параллельного контура определяется по формуле
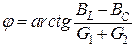 ,
,
где 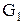 - активная проводимость первой ветви (
- активная проводимость первой ветви ( 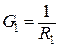 );
);
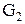 - активная проводимость второй ветви (
- активная проводимость второй ветви ( 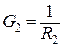 ).
).
Так как при резонансе токов 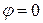 , то
, то 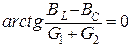 и из этого следует, что
и из этого следует, что
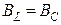 .
.








