Угол j всегда откладывается от вектора тока к вектору напряжения . Положительный угол j откладывается против часовой стрелки, отрицательный – по часовой стрелке.
Расчет электрических цепей переменного тока
Расчет производится с использованием тех же методов, что и цепей постоянного тока (отличие заключается в использовании комплексных чисел).
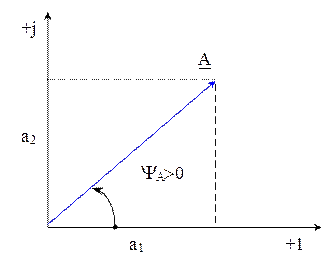
Любому вектору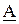 
, расположенному на комплексной плоскости, однозначно соответствует комплексное число , 
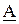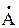которое может быть записано в трех формах: алгебраической, тригонометрической и показательной.
В электротехнике в отличие от математики мнимую единицу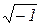 
обозначают j, так как буква i принята для обозначения мгновенного значения тока.
Алгебраическая форма записи комплексного числа
,
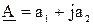где а1- проекция вектора на ось действительных чисел (+1,Re);
а2- проекция вектора на ось мнимых чисел (+j,Jm).
Тригонометрическая форма записи
,
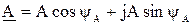где А – длина вектора;
три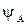 
- угол наклона вектора к оси действительных чисел.
Показательная форма записи
,
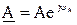где А – модуль комплексного числа (соответствует действующему значению синусоидальной функции или длине вектора);
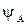- аргумент комплексного числа (соответствует углу наклона вектора к оси действительных чисел или начальной фазе синусоидальной функции);
е – основание натурального логарифма е=2,718.
Если аргумент комплексного числа положительный, то угол откладывается против направления движения часовой стрелки, если отрицательный – по часовой стрелке. Комплексные числа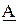 
и 
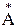называют сопряженными, если их модули равны, а аргументы равны и противоположны по знаку:
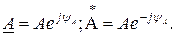
Алгебраические операции с комплексными числами
При суммировании и вычитании комплексных чисел используют только алгебраическую форму записи;
.
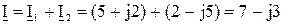При выполнении действия суммируют отдельно действительные и мнимые части комплексного числа.
При умножении комплексных чисел можно использовать как алгебраическую, так и показательную формы записи
а)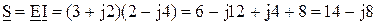 
б)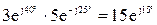 
.
При умножении комплексных чисел в показательной форме модули перемножают, а аргументы складывают.
При делении комплексных чисел можно использовать как показательную, так и алгебраическую формы записи
а)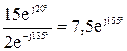 
.
При делении комплексных чисел в показательной форме их модули делят, а аргументы вычитают.
б)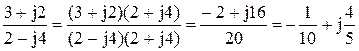 
.
При выполнении действия при алгебраической форме записи числитель и знаменатель умножают на сопряженное знаменателю комплексное число. Этот прием позволяет избавиться от мнимой единицы в знаменателе. Полезно знать следующие соотношения:
.
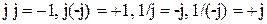Анализ электрического состояния цепи переменного тока
В состав простых цепей переменного тока обычно входят резистивные элементы 
, катушки индуктивности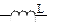 
, конденсаторы 
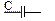и элементы, соединенные магнитной или емкостной связью с другими цепями. Прежде чем рассмотреть общий случай, когда цепь содержит все перечисленные элементы, проведем анализ простейших цепей.
Цепь с резистивным элементом
В резистивных элементах электрическая энергия преобразуется в тепловую. Эти элементы характеризуются значением сопротивления R, которое называется активным. Все параметры электрической цепи, обусловленные наличием сопротивления в цепи переменного тока, называются активными. Например, активная составляющая тока и напряжения (Ia, Ua).
Сопротивление резистивного элемента в цепи переменного тока может отличаться от сопротивления этого элемента в цепи постоянного тока. Это различие обусловлено поверхностным эффектом и зависит от частоты. При частоте 50 Гц различие между значениями сопротивления можно не учитывать. Поверхностный эффект проявляется в том, что плотность тока у поверхности проводника всегда больше, чем во внутренних участках его сечения из-за различия индуктивных сопротивлений.
Если предположить, что цепь с резистором подключена на синусоидальное напряжение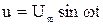 
, то мгновенное значение можно найти по закону Ома:
; 
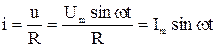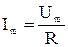– амплитуда тока.