Теорема 1. Вероятность суммы двух несовместных событий равна сумме
тема « Сложение и умножение вероятностей ».
Цели: 1.Ввести теоремы сложения и умножения вероятностей.
2.Рассмотреть примеры вероятностей на сложение и умножение.
I. Объяснение нового материала.
Теорема 1. Вероятность суммы двух несовместных событий равна сумме
вероятностей этих событий, т.е. Р(А+В)=Р(А)+Р(В).
Задача 1. В ящике лежат 50 шаров. 18 синих шаров, 12 красных и 20 желтых. Наугад вынимают 1 шар. Найти вероятность, что шар оказался не желтым?
а) Событие А – шар оказался синим: Р(А) =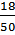 
б) Событие В – шар оказался красным: Р(В) =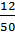 
События А и В одновременно произойти не могут. Говорят, что события А и В – несовместные .
Два события называются несовместными, если наступление одного из них исключает наступление другого.
Тогда вероятность, что шар оказался не желтым будет равна Р(С) = Р(А) + Р(В), т.е.
+ = 
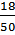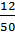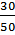= 0,6
Если наступает только одно из двух несовместных событий, то вероятности складываются.
Теорема 2. Произведением событий А и В (которые могут произойти в одном
испытании) называется событие А*В, состоящее в том, что оба
события произошли одновременно.
Р (АВ)=Р(А)*Р(В).
Задача 2. В одном из двух ящиков находятся 10 шаров, из которых 7 красных и 3 желтых, а в другом - 15 шаров, из которых 5 красных и 10 желтых. Из каждого ящика наугад вынимают по одному шару. Найти вероятность того, что оба шара окажутся желтыми.
а) Событие А – из первого ящика вынимают желтый шар: Р(А) =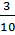 
б) Событие В – из второго ящика вынимают желтый шар: Р(В) =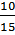 
События А и В являются независимыми, т.е. вытаскивание желтого шара из первого ящика никак не влияет на вытаскивание желтого шара из второго ящика.
Два события называются независимыми, если наступление одного из них не зависит от наступление другого.
Тогда вероятность, что оба шара окажутся желтым будет равна Р(С) = Р(А)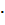 
Р(В), т.е.
= 
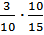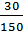= 0,2
Если наступают два независимых события, то вероятности умножаются.
Задача 3. Вероятность попадания в мишень одного стрелка равна 0,9, а другого – 0,8. Каждый сделал по одному выстрелу. Какова вероятность, что мишень будет поражена?
а) Событие А – первый стрелок попал в мишень
б) Событие В – второй стрелок попал в мишень
в) мишень поражена
События А и В являются независимыми. Но воспользоваться умножением вероятностей в этом случае нельзя, т.к. мишень будет поражена и при попадании в цель только одного стрелка. В этом случае считаем иначе. Находим противоположные события.
Вероятность, что промахнулся первый стрелок: Р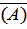 
= 1 – 0,9 = 0,1;
промахнулся второй стрелок: Р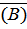 
= 1 – 0,8 = 0,2.
События А и В являются независимые, значит вероятность промаха обоих стрелков
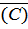Р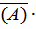 
= Р 
Р 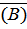, т.е. 0,1 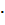0,2 = 0,02, следовательно, вероятность, что мишень будет
поражена Р(С) = 1 – 0,02 = 0,98
2.Закрепление: Образец выполнения задачи.
Задача 1. Стрелок делает по мишени два выстрела. Вероятность попадания по мишени при первом выстреле равна 0,8, а при втором 0,9. Найдите вероятность того: 1) что стрелок оба раза попадет по мишени; 2) стрелок оба раза промахнется.
Решение: А –событие стрелок попал по мишени при первом выстреле: Р(А) =0,8
В –событие стрелок попал по мишени при втором выстреле: р(В)=0,9. События А и В независимые.
1) С1-событие стрелок оба раза попал по мишени: С1=АВ по формуле Р(АВ)=Р(А)*Р(В) находим
Р(С1)=0,8*0,0,72.
2) С2- событие стрелок оба раза промахнется. Тогда нужно найти вероятность события противоположному событию А и В: С2=(1-Р(А))*(1-Р(В))=(1-0,8)*(1-0,9)=0,2*0,1=0,02.
Ответ: 1) 0,72, 2) 0,02.
Задача 2. Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Найти вероятность того, что: а) оба элемента выйдут из строя; б) оба элемента будут работать.
Решение. Пусть событие А – выход из строя первого элемента, В – выход из строя второго элемента. Эти события независимы по условию.
а) одновременное появление А и В есть событие АВ. Следовательно,
Р (АВ)=Р(А)*Р(В)=0,2*0,3=0,06.
б) Если работает первый элемент, то имеет место событие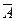 
, которое противоположное событию А; если работает второй элемент – событие В.
Найдем вероятности событий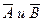 
: Р ( 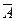)=1-Р(А)=1-0,2=0,8; Р( 
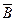)=1- Р(В)=1-0,3=0,7.
Тогда событие, состоящее в том, что будут работать оба элемента, есть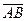 
и, значит
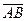Р 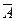( )= Р( )*Р( 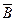)=0,8*0,7=0,56.
ЗАПОМНИ ФОРМУЛЫ! 
Домашнее задание.
Самостоятельная работа
Задачи на вычисление вероятностей
Задача 1. Какова вероятность появления четного числа очков (событие А) при одном бросании игрального кубика?
Задача 2. В урне 5 белых и 10 черных шаров. Шары тщательно перемешивают и затем наугад вынимают 1 шар. Какова вероятность того, что вынутый шар окажется белым?
Задача 3. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,19. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Задача 4. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20000 руб., на 10 билетов по 15000 руб., на 15-по 10000руб, на 25- по2000 руб. и на остальные ничего. Найдите вероятность того, что на купленный билет будет получен выигрыш не менее 10000руб.
Задача 5. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0,1. Вероятность того, что это окажется задача по теме «Параллелограмм», равна 0,6. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.