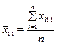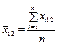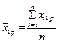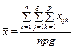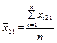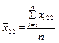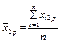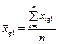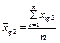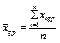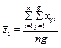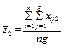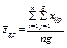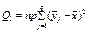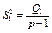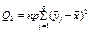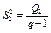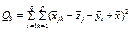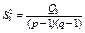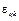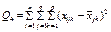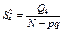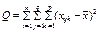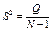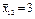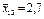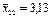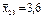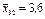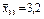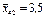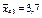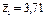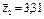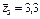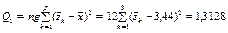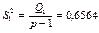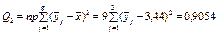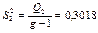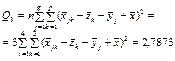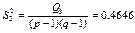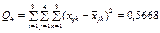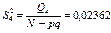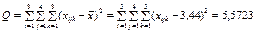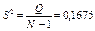Позначимо через конкретне значення ознаки Х, якого вона набуває при i-му експерименті, j-му рівні фактора A і k-му рівні фактора В.
Результат експерименту зручно подати у вигляді таблиці, яка поділена на блоки, в кожному з яких ураховується на певних рівнях факторів А і В їх вплив на конкретні значення ознаки 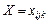 (табл. 3).
(табл. 3).
Виходячи з даних табл.,
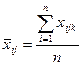 (474)
(474)
є середнім значенням ознаки Х для кожного блока;
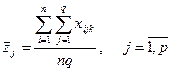 (475)
(475)
є середнім значенням ознаки Х за стовпцями;
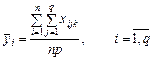 (476)
(476)
є середнім значенням ознаки Х за рядками;
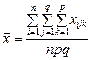 (477)
(477)
є загальною середньою ознакою Х;
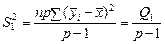 (478)
(478)
є виправленою дисперсією, яка зумовлена впливом фактора А на ознаку Х;
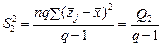 (479)
(479)
є виправленою дисперсією, яка зумовлена впливом фактора В на ознаку Х;
Таблиця 3
| Рівень | Рівень фактора А | Середня | Загальна | |||||||||
| А1 | А2 | ...... | Ар | |||||||||
| блочна середня | блочна середня | блочна середня | ||||||||||
| В1 | 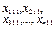
|
| 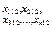
|
| ..... | 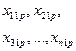
|
| 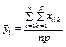
|
| |||
| В2 | 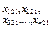
|
| 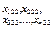
|
| ..... | 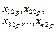
|
| 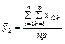
| ||||
| ............ | ................ | .................. | .................. | .................. | ..... | ................. | .................. | .................. | ||||
| Вg | 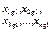
|
| 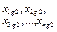
|
| ..... | 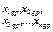
|
| 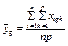
| ||||
| Середня величина за стовпцями |
|
| ..... |
| ||||||||
| Джерело, що спонукає до розсіювання | Сума квадратів відхилень | Число ступенів свободи | Статистичні оцінки дисперсій (виправлені дисперсії) | |||||||||
| Фактор А |
| р – 1 |
| |||||||||
| Фактор В |
| q – 1 |
| |||||||||
| Одночасна дія факторів А і В |
| (p – 1)(q – 1) |
| |||||||||
| Дія випадкової компоненти |
| N – pq |
| |||||||||
| Загальне відхилення |
| N – 1 |
| |||||||||

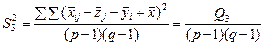 (480)
(480)
є виправленою дисперсією, яка зумовлена одночасним впливом на ознаку Х факторів А і В;
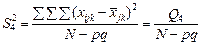 (481)
(481)
є виправленою дисперсією, яка зумовлена впливом на ознаку Х інших, не головних факторів.
Обчислюються спостережувані значення критерію
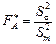 ;
; 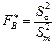 ;
; 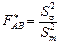 .
.
При рівні значущості a визначають критичні точки:
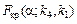 ,
, 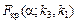 ,
, 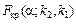 .
.
Якщо:
1) 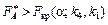 , то нульова гіпотеза про відсутність впливу фактора А відхиляється;
, то нульова гіпотеза про відсутність впливу фактора А відхиляється;
2) 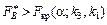 , то нульова гіпотеза про відсутність впливу фактора В відхиляється;
, то нульова гіпотеза про відсутність впливу фактора В відхиляється;
3) 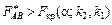 , то нульова гіпотеза про відсутність спільного впливу факторів А і В відхиляється.
, то нульова гіпотеза про відсутність спільного впливу факторів А і В відхиляється.
Приклад. У чотирьох різних лабораторіях здійснювався експеримент з опріснення морської води за допомогою трьох опріснювачів. Кожний експеримент для кожного опріснювача в кожній лабораторії проводився тричі. Наслідки опріснювання, виражені у відсотках, наведені в таблиці:
| Ступінь впливу В | Ступінь впливу А | ||
| А1 | А2 | А3 | |
| В1 | 3,6; 3,9; 4,1 | 2,9; 3,1; 3,0 | 2,7; 2,5; 2,9 |
| В2 | 4,2; 4,0; 4,1 | 3,3; 2,9; 3,2 | 3,7; 3,5; 3,6 |
| В3 | 3,8; 3,5; 3,6 | 3,6; 3,7; 3,5 | 3,2; 3,0; 3,4 |
| В4 | 3,4; 3,2; 3,2 | 3,4; 3,6; 3,5 | 3,6; 3,8; 3,7 |
При рівні значущості a = 0,05 перевірити, чи існує вплив факторів А і В, а також спільної дії А і В на кінцевий результат експерименту.
Розв’язання. Використовуючи табл. 3, дістанемо табл. 4:
Таблиця 4
| Ступінь впливу | Ступінь впливу фактора А | Середня | Загальна | ||||||||
| А1 | А2 | А3 | |||||||||
| перший рівень | блочна середня | другий рівень | блочна середня | третій рівень | блочна середня | ||||||
| В1 | Перший рівень | 3,6; 3,8; 4,1 | 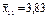
| 2,9; 3,1; 3,0 |
| 2,7; 2,5; 2,9 |
| 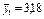
| |||
| В2 | Другий рівень | 4,2; 4,0; 4,1 | 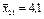
| 3,3; 2,9; 3,2 |
| 3,7; 3,5; 3,6 |
| 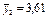
| 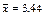
| ||
| В3 | Третій рівень | 3,8; 3,5; 3,6 | 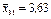
| 3,6; 3,7; 3,5 |
| 3,2; 3,0; 3,4 |
| 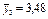
| |||
| В4 | Четвертий рівень | 3,4; 3,2; 3,2 | 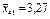
| 3,4; 3,6; 3,5 |
| 3,6; 3,8; 3,7 |
| 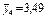
| |||
| Середня величина |
|
|
| ||||||||
| Джерело, що спонукає | Сума квадратів відхилень | Число ступенів свободи | Статистичні оцінки дисперсії | ||||||||
| Фактор А |
| p – 1 = 2 |
| ||||||||
| Фактор B |
| q – 1 = 3 |
| ||||||||
| Одночасний вплив |
| (p – 1)´ |
| ||||||||
| Вплив випадкових |
| N – pq = 24 |
| ||||||||
| Загальна дисперсія |
| N – 1 = 35 |
| ||||||||

Визначимо спостережувані значення статистичних критеріїв за кожним фактором А, В та їх сумісної дії:
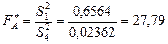 ;
;
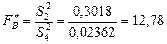 ;
;
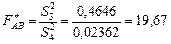 ;
;
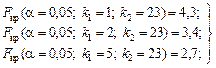 за таблицею (додаток 7).
за таблицею (додаток 7).
Висновок. Оскільки 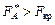 , то нульова гіпотеза про відсутність впливу фактора А відхиляється, аналогічно
, то нульова гіпотеза про відсутність впливу фактора А відхиляється, аналогічно 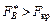 ,
, 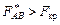 , а це інформує про те, що нульова гіпотеза про відсутність впливу фактора В, а також сумісної дії факторів А і В також відхиляється.
, а це інформує про те, що нульова гіпотеза про відсутність впливу фактора В, а також сумісної дії факторів А і В також відхиляється.