Якщо , то нульова гіпотеза про вплив фактора на результати досліджень відхиляється, а коли , то цим самим підтверджується вплив фактора на ознаку Х.
Тема для самостійного опрацювання 4
Елементи дисперсійного аналізу
1. Загальна інформація
Дисперсійний аналіз був створений спочатку для статистичної обробки агрономічних дослідів. В наш час його також використовують як в економічних експериментах, так і технічних, соціальних.
Сутність цього аналізу полягає в тому, що загальну дисперсію досліджуваної ознаки розділяють на окремі компоненти, які обумовлені впливом певних конкретних чинників. Істотність їх впливу на цю ознаку здійснюється методом дисперсійного аналізу.
Відповідно до дисперсійного аналізу будь-який його результат можна подати у вигляді суми певної кількості компонент. Так, наприклад, якщо досліджується вплив певного чинника на результат експерименту, то модель, що описує структуру останнього, можна подати так:
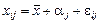 , (467)
, (467)
де 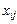 — значення ознаки Х, одержане при i-му експерименті на j-му рівні фактора. Під рівнем фактора розуміють певну його міру. Наприклад, якщо фактором є добрива, які вносяться в ґрунт з метою збільшення врожайності сільськогосподарської культури, то рівнем фактора в цьому разі є кількість добрива, що вноситься в ґрунт;
— значення ознаки Х, одержане при i-му експерименті на j-му рівні фактора. Під рівнем фактора розуміють певну його міру. Наприклад, якщо фактором є добрива, які вносяться в ґрунт з метою збільшення врожайності сільськогосподарської культури, то рівнем фактора в цьому разі є кількість добрива, що вноситься в ґрунт; 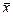 — загальна середня величина ознаки Х;
— загальна середня величина ознаки Х; 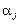 — ефект впливу фактора на значення ознаки Х на j-му рівні;
— ефект впливу фактора на значення ознаки Х на j-му рівні; 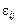 — випадкова компонента, що впливає на значення ознаки Х в i-му експерименті на j-му рівні.
— випадкова компонента, що впливає на значення ознаки Х в i-му експерименті на j-му рівні.
При цьому 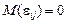 і
і 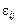 як випадковi величини мають закон розподілу ймовірностей
як випадковi величини мають закон розподілу ймовірностей 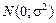 і між собою незалежні (
і між собою незалежні ( 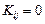 ).
).
Складнішою моделлю аналізу є вивчення впливу на результати експерименту кількох факторів. Зокрема при аналізі впливу двох факторів структура моделі набуває такого вигляду:
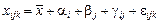 , (468)
, (468)
де 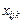 — значення ознаки Х в i-му експерименті на j-му рівні впливу фактора А і на k-му рівні впливу фактора В;
— значення ознаки Х в i-му експерименті на j-му рівні впливу фактора А і на k-му рівні впливу фактора В; 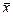 — загальна середня величина ознаки Х;
— загальна середня величина ознаки Х; 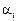 — ефект впливу фактора А на i-му рівні;
— ефект впливу фактора А на i-му рівні; 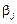 — ефект впливу фактора B на j-му рівні;
— ефект впливу фактора B на j-му рівні; 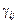 — ефект одночасного впливу факторів А і В;
— ефект одночасного впливу факторів А і В; 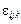 — випадкова компонента.
— випадкова компонента.
У разі проведення дисперсійного аналізу досліджуваний масив даних, одержаних під час експерименту, поділяють на певні групи, які різняться дією на результати експерименту певних рівнів факторів.
Вважається, що досліджувана ознака має нормальний закон розподілу, а дисперсії в кожній окремій групі здобутих значень ознаки однакові. Ці припущення необхідно перевірити.
2. Однофакторний дисперсійний аналіз
Нехай потрібно дослідити вплив на ознаку Х певного одного фактора. Результати експерименту ділять на певне число груп, які відрізняються між собою ступенем дії фактора.
Для зручності в проведенні необхідних обчислень результати експерименту зводять в спеціальну таблицю:
Таблиця 1
| Ступінь впливу фактора (групи) | Спостережуване значення ознаки Х | Групові середні | Загальна середня |
| 1 | 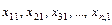
| 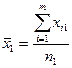
|
|
| 2 | 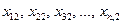
| 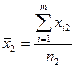
| |
| 3 | 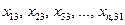
| 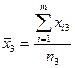
| |
| . . . | ................................ ................................ ................................ | ........................ ........................ ......................... | |
| р | 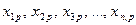
| 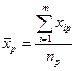
|
Відповідно до моделі однофакторного дисперсійного аналізу необхідно визначити дві дисперсії, а саме: міжгрупову (дисперсію групових середніх), зумовлену впливом досліджуваного фактора на ознаку Х, і внутрішньогрупову, зумовлену впливом інших випадкових факторів.
Загальна дисперсія розглядається як сума квадратів відхилень:
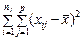 .
.
Тоді поділ загальної дисперсії на компоненти здійснюється так:
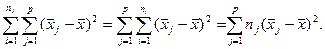
Таким чином, дістаємо:
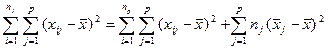 . (469)
. (469)
Для того щоб мати виправлені дисперсії, необхідно кожну зі здобутих сум поділити на число ступенів свободи.
Так, для загальної дисперсії 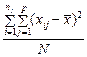 виправлена дисперсія дорівнюватиме
виправлена дисперсія дорівнюватиме
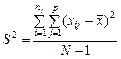 . (470)
. (470)
Виправлена дисперсія 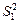 , що характеризує розсіювання всередині групи, зумовлене впливом випадкових факторів, обчислюється за формулою:
, що характеризує розсіювання всередині групи, зумовлене впливом випадкових факторів, обчислюється за формулою:
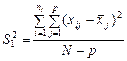 , (471)
, (471)
де 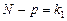 є числом ступенів свободи для
є числом ступенів свободи для 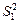 , оскільки при цьому використовується р співвідношень при обчисленні групових середніх
, оскільки при цьому використовується р співвідношень при обчисленні групових середніх 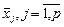 .
.
Виправлена дисперсія 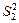 , що характеризує розсіювання групових середніх
, що характеризує розсіювання групових середніх 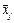 відносно загальної середньої
відносно загальної середньої 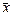 , яке викликане впливом фактора на результат експерименту ознаки Х, обчислюється за формулою:
, яке викликане впливом фактора на результат експерименту ознаки Х, обчислюється за формулою:
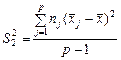 , (472)
, (472)
де 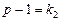 — це число ступенів свободи для
— це число ступенів свободи для 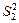 , оскільки групові середні варіюють відносно однієї загальної середньої
, оскільки групові середні варіюють відносно однієї загальної середньої 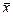 .
.
Завдання виявлення впливу фактора на наслідки експерименту полягає в порівнянні виправлених дисперсій 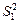 ,
, 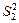 . І справді, якщо досліджуваний фактор не впливає на значення ознаки Х, то в цьому разі
. І справді, якщо досліджуваний фактор не впливає на значення ознаки Х, то в цьому разі 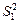 і
і 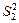 можна розглядати як незалежні оцінки загальної дисперсії D. І навпаки, якщо відношення
можна розглядати як незалежні оцінки загальної дисперсії D. І навпаки, якщо відношення 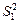 i
i 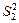 істотне, то в цьому разі вибірки слід вважати здійсненими з різних сукупностей, тобто з сукупностей з різним рівнем впливу фактора.
істотне, то в цьому разі вибірки слід вважати здійсненими з різних сукупностей, тобто з сукупностей з різним рівнем впливу фактора.
Порівняння двох дисперсій ґрунтується на перевірці правильності нульової гіпотези: 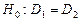 — про рівність дисперсій двох вибірок.
— про рівність дисперсій двох вибірок.
За статистичний критерій вибирається випадкова величина
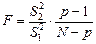 , (473)
, (473)
що має розподіл Фішера—Снедекора з 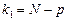 ,
, 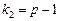 ступенями свободи.
ступенями свободи.
За значеннями a, 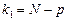 ,
, 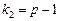 , знаходимо критичну точку (додаток 7).
, знаходимо критичну точку (додаток 7).
Спостережуване значення критерію обчислюється за формулою (473).
Якщо 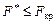 , то нульова гіпотеза про вплив фактора на результати досліджень відхиляється, а коли
, то нульова гіпотеза про вплив фактора на результати досліджень відхиляється, а коли 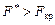 , то цим самим підтверджується вплив фактора на ознаку Х.
, то цим самим підтверджується вплив фактора на ознаку Х.
Результати спостережень та обчислення статистичних оцінок зручно подати в упорядкованому вигляді за допомогою табл. 2.
Таблиця 2
| Рівень фактора (групи) | Спостережуване значення ознаки Х | Групові середні | Загальна середня |
| 1 | 
| 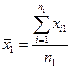
| |
| 2 | 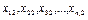
| 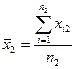
| 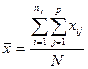 , ,
|
| . . . | .................................... .................................... .................................... | ........................ ........................ ........................ | 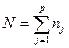
|
| р | 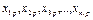
| 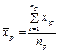
| |
| Вид варіацій ознаки | Сума квадратів відхилень | Число ступенів свободи | Статистичні оцінки дисперсії |
| внутрішньогрупова | 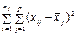
| N – p | 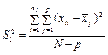
|
| між- групова | 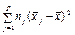
| p – 1 | 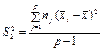
|
| загальна | 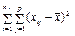
| N – 1 | 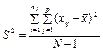
|
Приклад 1. Ступінь впливу каталізатора на кінцевий продукт заданої хімічної реакції, наведеної в таблиці.
| Ступінь впливу каталізатора | Кінцевий продукт хімічної реакції |
| 1 | 3,2; 3,1; 3,1; 2,8; 3,3; 3,0 |
| 2 | 2,6; 3,1; 2,7; 2,9; 2,7; 2,8 |
| 3 | 2,9; 2,6; 3,0; 3,1; 3,0; 2,8 |
| 4 | 3,7; 3,4; 3,2; 3,3; 3,5; 3,3 |
| 5 | 3,0; 3,4; 3,2; 3,5; 2,9; 3,1 |
З’ясувати, чи істотно впливає каталізатор на кінцевий продукт хімічної реакції при a = 0,001.
Розв’язання. Використовуючи табл. 2 і виконавши відповідні обчислення, дістанемо
| Ступінь впливу каталізатора | Спостережуване значення (кінцевий продукт) | Групові середні | Загальна середня |
| 1 | 3,2; 3,1; 3,1; 2,8; 3,3; 3,0 | 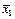 =3,083 =3,083
| |
| 2 | 2,6; 3,1; 2,7; 2,9; 2,7; 2,8 | 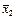 =2,8 =2,8
| |
| 3 | 2,9; 2,6; 3,0; 3,1; 3,0; 2,8 | 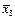 =2,9 =2,9
| 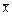 = 3,073 = 3,073
|
| 4 | 3,7; 3,4; 3,2; 3,3; 3,5; 3,3 | 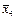 =3,4 =3,4
| |
| 5 | 3,0; 3,4; 3,2; 3,5; 2,9; 3,1 | 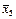 =3,18 =3,18
| |
| Вид варіації ознаки | Сума квадратів відхилень | Число ступенів свободи | Статистичні оцінки дисперсій |
| внутрішньогрупова | 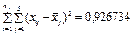
| 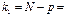 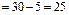
| 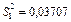
|
| міжгрупова | 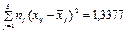
| 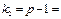 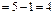
| 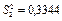
|
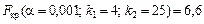 ;
;
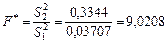 .
.
Висновок. Оскільки 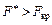 , то вплив каталізатора на кінцевий продукт хімічної реакції є істотним.
, то вплив каталізатора на кінцевий продукт хімічної реакції є істотним.
3. Двофакторний дисперсійний аналіз
Нехай необхідно визначити вплив двох факторів А і В на певну ознаку Х. Для цього необхідно, щоб дослід здійснювався при фіксованих рівнях факторів А і В, а також їх одночасній дії на ознаку. При цьому дослід здійснюватимемо n раз для кожного з рівнів факторів А і В.








