Нехай між змінними Х та Y теоретично існує певна лінійна залежність. Це твердження може ґрунтуватися на тій підставі, наприк­лад, що кореляційне поле для пар має такий вигляд (рис. 150).

Дата: 2025-06-02; Просмотры: 8
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

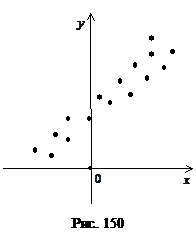Як бачимо, насправді між оз­наками Х і Y спостерігається не такий тісний зв’язок, як це передбачає функціональна залежність.

Окремі спостережувані значення y, як правило, відхилятимуться від передбаченої лінійної залежності під впливом випадкових збудників, які здебільшого є невідомими. Відхилення від передбаченої лінійної форми зв’язку можуть статися внаслідок неправиль­ної специфікації рівняння, тобто ще з самого початку неправильно вибране рівняння, що описує залежність між X і Y.

Будемо вважати, що специфікація рівняння вибрана правильно. Ураховуючи вплив на значення Y збурювальних випадкових факторів, лінійне рівняння зв’язку X і Y можна подати в такому вигляді:

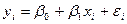, (485)

де 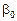, 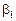є невідомі параметри регресії, 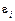є випадковою змінною, що характеризує відхилення y від гіпотетичної теоретичної регресії.

Отже, в рівнянні (485) значення «y» подається у вигляді суми двох частин: систематичної 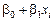і випадкової 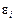. Параметри 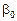, 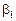є невідомими величинами, а 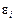є випадковою величиною, що має нормальний закон розподілу з числовими характеристиками: 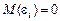, 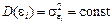. При цьому елементи послідовності 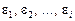є некорельованими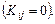

У результаті статистичних спостережень дослідник дістає характеристики для незалежної змінної х і відповідні значення залежної змінної у.

Отже, необхідно визначити параметри 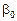, 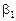. Але істинні значення цих параметрів дістати неможливо, оскільки ми користуємося інформацією, здобутою від вибірки обмеженого обсягу. Тому знайдені значення параметрів будуть лише статистичними оцінками істинних (невідомих нам) параметрів 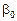, 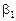. Якщо позначити параметри 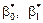, які дістали способом обробки вибірки, моделі

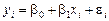(486)

відповідатиме статистична оцінка

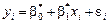. (487)

2.1. Визначення параметрів 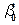, 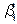. Якщо ми прийняли гіпотезу про лінійну форму зв’язку між ознаками Х і Y, то однозначно вибрати параметри 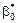, , 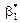які є точковими статистичними оцінками відповідно для параметрів 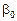, , 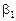практично неможливо. І справді, через кореляційне поле (рис. 150) можна провести безліч прямих. Тому необхідно вибрати такий критерій, за яким можна здійснити вибір параметрів , .

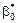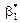На практиці найчастіше параметри 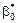, 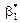визначаються за методом найменших квадратів, розробка якого належить К. Гауссу і П. Лапласу. Цей метод почали широко застосовувати в економіко-статистичних обчисленнях, відколи була створена теорія регресії.

Відповідно до цього методу рівняння лінійної парної регресії 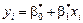необхідно вибрати так, щоб сума квадратів відхилень спостережуваних значень від лінії регресії була б мінімальною.

, :

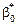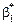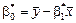; (493)

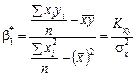. (494)

Помноживши ліву і праву частини (494) на 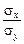, дістанемо:

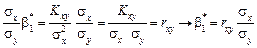, (495)

де rxy —парний коефіцієнт кореляції між ознаками X і Y. Тоді

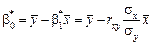. (496)

З урахуванням (495), (496) рівняння лінійної парної регресії набере такого вигляду:

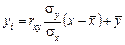(497)

або

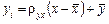, (498)

де 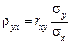і називають коефіцієнтом регресії.

Приклад. Залежність розчинності уі тіосульфату від температури хі наведено парним статистичним розподілом вибірки:

Y = yi 33,5 37,0 41,2 46,1 50,0 52,9 56,8 64,3 69,9
X = xi 0 10 20 30 40 50 60 70 80

Потрібно:

1) побудувати кореляційне поле залежності ознаки Y від X;

2) визначити точкові незміщені статистичні оцінки 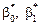. Обчислити rxy ;

3) побудувати графік лінії регресії.

Розв’язання. 1) кореляційне поле залежності ознаки Y від X має такий вигляд (рис. 152).

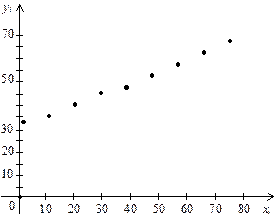
Рис. 152

З рис. 152 бачимо, що зі збільшенням значень ознаки 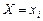залежна зміна 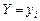має тенденцію до збільшення.

Тому припускаємо, що між ознаками Х та Y існує лінійна функціональна залежність

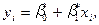
2) для визначення параметрів 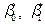скористаємося таблицею, що має такий вигляд:

№ з/п хі уі 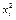хі уі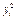
1 0 33,5 0 0 1122,25
2 10 37,0 100 307 1369,00
3 20 41,2 400 824 1697,44
4 30 46,1 900 1383 2125,21
5 40 50,0 1000 2000 2500,00
6 50 52,9 2500 2645 2798,41
7 60 56,8 3600 3408 3226,24
8 70 64,3 4900 4501 4134,49
9 80 69,9 6400 5592 4886,01
Σ 360 451,7 20400 20723 23859,05

Скориставшись формулами (494), (496), дістанемо

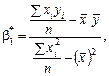
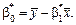
Оскільки n = 9,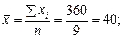

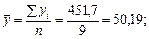
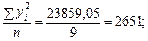
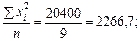
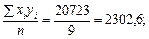
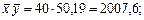
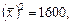одержимо:

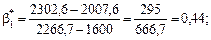
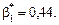
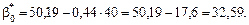
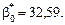
Отже, рівняння регресії буде таким:

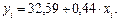
Для обчислення 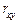необхідно знайти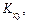

;

;

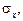
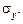
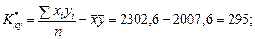
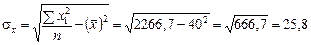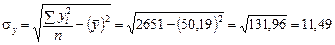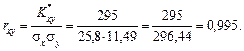
Як бачимо, коефіцієнт кореляції близький за своїм значенням до одиниці, що свідчить про те, що залежність між Х та Y є практично лінійною.

Графік парної лінійної функції регресії подано на рис. 153.

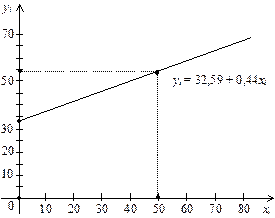
Рис. 153

Якщо параметри 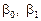рівняння (486) — сталі величини, то 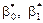, які обчислені шляхом обробки реалізованої вибірки, є випадковими величинами і виконують функцію точкових статистичних оцінок для них.