Деление с остатком
Число 13 не делится на 5. Наибольшее число, которое делится на 5 и не превосходит 13, равно 10 = 5 · 2. Таким образом, 13 = 5 · 2 + 3, и мы скажем, что в результате деления 13 на 5 получается частное 2 и остаток 3. Оказывается, любое число a можно разделить с остатком на любое число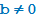 
. А именно, найдутся два числа q и r такие, что 
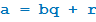, и при этом будет выполнено неравенство 
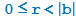. Число q называется частным, а число r - остатком от деления a на b.
Если r = 0, то есть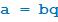 
, то a делится на b.
Упражнение
Найдите частное и остаток от деления:
а) 7 на 2;
б) 15 на 4;
в) 2012 на 5;
г) 1001 на 13;
д) 9 на 8;
е) 8 на 9.
Остаток от деления любого нечётного числа на 2 равен единице. Вот почему всякое нечётное число может быть записано в виде 2n + 1. Остатки оказываются полезными во многих ситуациях. Допустим, в ходе решения задачи вам нужно доказать, что равенство 
не может выполняться ни при каких целых числах n и k. Рассуждаем следующим образом.
Число n при делении на 3 может давать остатки 0, 1 или 2. Иными словами, возможны три случая: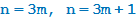 
или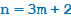 
. Какие остатки при делении на 3 будут у числа 
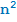? Давайте посмотрим, что получается в каждом из трёх случаев.
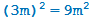(остаток 0); 
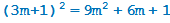(остаток 1);
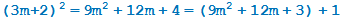(остаток 1).
Таким образом, квадрат целого числа при делении на 3 не может давать остаток 2. Следовательно, равенство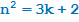 
действительно невозможно ни при каких n и k.
Упражнение 1
Докажите, что число 100 . . . 004 (между 1 и 4 стоит любое число нулей) не является квадратом целого числа.
Упражнение 2
Докажите, что квадрат целого числа при делении на 4 может давать только два остатка: 0 и 1.
Упражнение 3
Докажите, что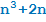 
делится на 3.
Каноническое разложение
Всякое число делится на 1 и на само себя. Если натуральное число p не равно 1 и не имеет других натуральных делителей, кроме 1 и p, то такое число p называется простым.
Вот первые несколько простых чисел: 2, 3, 5, 7, 11, 13, 17, 19. Число 2 — единственное чётное простое число.
Число, не равное 1 и не являющееся простым, называется составным. Например, 15 — составное число (оно делится на 3). Число 1036 — тоже составное (оно чётное). Единица не является ни простым числом, ни составным.
Упражнение
Число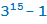 
является составным. Почему?
Оказывается, всякое число можно разложить на простые множители. Например:
Такое разложение единственно с точностью до порядка множителей и называется каноническим разложением. Утверждение о существовании и единственности канонического разложения носит название основной теоремы арифметики.
Каноническое разложение даёт полную картину делителей данного числа (и, в частности, позволяет найти их количество). Именно, пусть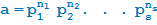 
— каноническое разложение числа a. Тогда каноническое разложение любого делителя числа a состоит из простых множителей, входящих в набор 
показатели степени которых не превосходят соответственно чисел 
. Например, любой делитель числа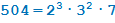 
имеет вид 
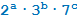, где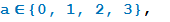 
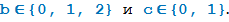
Отвечаем на вопрос упражнения: 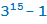является составным числом, т.к. при умножении нескольких раз числа 3 мы получим число, в конце которого стоит цифра 9, 7, 1 или 3. При вычитании из каждой из них единицы, всегда получаем чётное число, а, значит, всё число делится на 2, т.е. является составным.
Упражнение 1
Пусть p - простое число. Сколько делителей у числа:
а)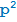 
;
б)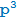 
;
в)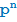 
?
Упражнение 2
Пусть p и q — простые числа. Сколько делителей у числа:
а)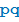 
;
б)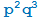 
;
в)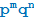 
?
Упражнение 3
Обобщив рассуждения пункта в) предыдущего упражнения, покажите, что количество делителей числа 
равно:
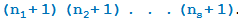
Найдите, сколько делителей имеет число 504.
Упражнение 4
Найдите канонические разложения чисел 540 и 252. С помощью полученных разложений найдите НОД (540, 252) — наибольший общий делитель этих чисел.