Конспект по теме «Теория чисел»
Числовые множества
В данном разделе мы определим числовые множества, необходимые для задачи 19. Введённую терминологию нужно твёрдо знать!
Натуральные числа — это числа 1, 2, 3 и т.д. Натуральные числа мы используем для счёта, а счёт начинается с единицы. Множество натуральных чисел обозначается N.
Целые числа — это числа 0, ±1, ±2, ±3 и т.д. Таким образом, целые числа — это нуль и «плюс-минус натуральные». Натуральные числа являются целыми положительными числами. Множество целых чисел обозначается Z.
Рациональные числа — это всевозможные дроби 
с целыми m и n (при этом, конечно, 
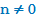; чтобы избежать данной оговорки, говорят также, что m — целое, а n — натуральное). Любое целое число является в то же время рациональным (например, 
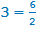). Однако число 
не является целым. Множество рациональных чисел обозначается Q.
Делимость
Понятие делимости относится к целым числам (в частности, к натуральным). Начиная с этого момента все числа считаются целыми. Если в каком-то случае это окажется не так, мы сделаем специальную оговорку.
Целые числа мы обозначаем a, b, c, . . , k, l, m, n, . . , x, y, z, то есть используем все строчные буквы латинского алфавита.
Вы прекрасно знаете, что число 12 делится на 4, но не делится на 5. Каково формальное определение делимости? Вот оно:
· Число a делится на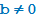 
, если найдётся число c такое, что 
.
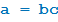Если a делится на b, то число b называется делителем числа a. Например, число 12 имеет шесть делителей: это 1, 2, 3, 4, 6 и 12.
Пример
Докажите, что если числа a и b делятся на c, то a + b делится на c.
Решение:
Т.к.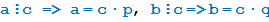 
. Значит,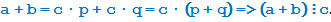 
Чётность
Соображения, связанные с чётностью или нечётностью, часто фигурируют в задачах 19. Поэтому необходимые факты имеет смысл отметить особо. Определение:
· Число называется чётным, если оно делится на 2.
· Число называется нечётным, если оно не делится на 2.
Вот все чётные числа: 0, ±2, ±4, ±6, . . .
Если a чётно, то оно имеет вид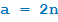 
.
А вот все нечётные числа: ±1, ±3, ±5, . . .
Ясно, что если a нечётно, то оно имеет вид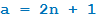 
.
Следующие утверждения весьма очевидны, и вы можете использовать их при решении задачи 19 (никто от вас не потребует их доказательства). Но вы можете доказать их в качестве упражнения.
