Задачи с использованием элементов комбинаторики
В этих задачах ответ также определяется по формуле P(A) = m/n, но подсчет числа n всех возможных событий и числа mблагоприятствующих событий заметно труднее, чем в предыдущих случаях. Для этого используют различные методы перебора вариантов и вспомогательные рисунки, таблицы, графы ("дерево возможностей"). Облегчить ситуацию могут правила сложения и умножения вариантов, а также готовые рецепты комбинаторики: формулы для числа перестановок, сочетаний, размещений.
Правило сложения: если некоторый объект A можно выбрать k способами, а объект B - l способами (не такими как А), то объект "или А или В" можно выбрать m + l способами.
Правило умножения: если объект А можно выбрать k способами, а после каждого такого выбора другой объект В можно выбрать (независимо от объекта А) l способами, то пары объектов А и B можно выбрать m·l способами.
Правило умножения еще называют "И-правилом", а правило сложения "ИЛИ-правилом". Не забывайте проверить независимость способов для "И" и несовместимость (не такими) для "ИЛИ".
Следующие задачи можно решать как перебором вариантов, так и с помощью формул комбинаторики. Я даю несколько способов решения для каждой задачи, потому что одним способом её можно решить быстро, а другим долго, и потому что кому-то понятнее один подход, а кому-то другой. Но это не значит, что обязательно нужно разбирать все способы. Лучше хорошо усвоить один любимый. Выбор за вами.
Задача 10
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
Решение
Способ I.
Можно выписать и рассмотреть все возможные исходы 3-ёх бросаний монеты: {ооо, ооp, оро, орр, роо, рор, рро, ррр}, где о - сокращение от "орёл", р - сокращение от "решка". Из перечисления видно, что n = 8, m = 1. (Благоприятствующее только ррр).
По формуле P(А) = 1/8 = 0,125.
Способ II.
Можно заметить, что условия испытания удовлетворяют схеме Бернулли с p = 1/2 и q = 1/2 и воспользоваться формулой
P(0) = C03·(1/2)0(1/2)(3-0) = 1·(1/2)3 = 1/8 = 0,125.
Ответ: 0,125
Задача 11
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно один раз.
Решение
Способ I.
Испытание то же и исходы те же, что в предыдущем случае: {ооо, ооp, оро, орр, роо, рор, рро, ррр}. Из перечисления видно, что n = 8, m = 3. (Благоприятствующие: {орр, рор, рро}).
По формуле P(А) = 3/8 = 0,375.
Способ II.
Условия испытания удовлетворяют схеме Бернулли с p = 1/2 и q = 1/2, значит по формуле
P(1) = C13·(1/2)1(1/2)(3-1) = 3·(1/2)1·(1/2)2 = 3/8 = 0,375.
Ответ: 0,375
Задача 12
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет хотя бы один раз.
Решение
Способ I.
Испытание то же и исходы те же, что в предыдущих случаях: {ооо, ооp, оро, орр, роо, рор, рро, ррр}. Из перечисления видно, что n = 8, m = 7. (Благоприятствующие все, кроме ооо).
По формуле P(А) = 7/8 = 0,875.
Способ II.
По формуле Бернулли с учетом правила сложения (хотя бы 1 из 3-х = или 1, или 2, или 3)
P(А) = P(1) + P(2) + P(3) = C13·(1/2)1(1/2)(3-1) + C23·(1/2)2(1/2)(3-2) + C33·(1/2)3(1/2)(3-3) = (3 + 3 + 1)·(1/2)3 = 7/8= 0,875.
Способ III.
Событие "орел выпадет хотя бы один раз" противоположно событию "орел не выпадет ни разу." Вероятность последнего равна 0,125. Мы определили её в задаче 10.
Значит P(A) = 1 - 0,125 = 0,875 по формуле для вероятности противоположного события.
Ответ: 0,875
Задача 13
В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орел не выпадет ни разу.
Решение
Воспользуемся правилом умножения для независимых испытаний.
При каждом бросании возможны 2 исхода, значит при 4-ех бросаниях возможны 2·2·2·2 = 16 исходов.
При каждом бросании орел не выпадет одним способом, значит при 4-ех бросаниях он не выпадет 1·1·1·1 = 1 одним способом.
По формуле P(А) = 1/16 = 0,0625.
Ответ: 0,0625
Замечание: Конечно, эту задачу можно было бы решить любым из способов, рассмотренных раньше. Но чем больше число возможных исходов, тем дольше и бессмысленнее решать перебором вариантов.
(Для тех, кто иначе не умеет или хочет проверить более короткое решение более длинным, всё же напишу: {oооо, oооp, oоро, oорр, oроо, oрор, oрро, oррр, pооо, pооp, pоро, pорр, pроо, pрор, pрро, pррр}.)
Cамый лучший способ при большом числе бросаний - формула Бернулли. Попробуйте применить её в этой задаче самостоятельно.
Задача 14
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Решение
Способ I.
Для одной кости может быть 6 разных исходов испытания (выпадение очков 1,2,...,6) и для другой - 6 исходов независимых от первой. Общее число возможных исходов при бросании двух костей определим по правилу умножения n = 6×6 = 36.
Чтобы определить число благоприятствующих исходов, посмотрим из каких слагаемых получается сумма 8:
1 + 7 = 8; 2 + 6 = 8; 3 + 5 = 8; 4 + 4 = 8; 5 + 3 = 8; 6 + 2 = 8; 7 + 1 = 8.
Первый и последний варианты являются в нашем случае невозможными событиями, числа 7 нет на обычных игральных костях. Остальные реализуются, если на одной кости выпадает первое слагаемое, а на другой кости - второе. Благоприятствующие исходы
{"2и6", "3и5", "4и4", "5и3", "6и2"}, всего их m = 5.
По формуле P(A) = 5/36 = 0,138889 ≈ 0,14.
Способ II.
Для этой задачи хорошо считать варианты с помощью таблички.
| 1 + 1 | 2 + 1 | 3 + 1 | 4 + 1 | 5 + 1 | 6 + 1 |
| 1 + 2 | 2 + 2 | 3 + 2 | 4 + 2 | 5 + 2 | 6 + 2 |
| 1 + 3 | 2 + 3 | 3 + 3 | 4 + 3 | 5 + 3 | 6 + 3 |
| 1 + 4 | 2 + 4 | 3 + 4 | 4 + 4 | 5 + 4 | 6 + 4 |
| 1 + 5 | 2 + 5 | 3 + 5 | 4 + 5 | 5 + 5 | 6 + 5 |
| 1 + 6 | 2 + 6 | 3 + 6 | 4 + 6 | 5 + 6 | 6 + 6 |
Ответ: 0,14
Замечание: Правила округления мы повторяли при решении задачи B1.
Задача 15
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
Решение
Способ I.
Для одной кости может быть 6 разных исходов испытания (выпадение очков 1,2,...,6), и для другой - 6 исходов, и для третьей - 6 исходов, независимых друг от друга. Общее число возможных исходов при бросании трёх костей определим по правилу умножения n = 6×6×6 = 216.
Чтобы определить число благоприятствующих исходов, посмотрим, из каких 3-х слагаемых можно получить число 7. Вспомним, что от перестановки мест слагаемых сумма не меняется.
или 7 = 1 + 1 + 5 (3 перестановки) или 1 + 2 + 4 (6 перестановок) или 1 + 3 + 3 (3 перестановки) или 2 + 2 + 3 (3 перестановки).
Таким образом, по правилу сложения m = 3 + 6 + 3 + 3 = 15 способов получить 7, как сумму очков на 3-х костях.
По формуле P(A) = 15/216 = 0,069444444 ≈ 0,07.
(Подробнее о расчете m: Сначала определяем из каких слагаемых может состоять число 7, например, по схеме
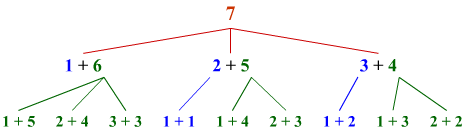 ,
,
и располагаем слагаемые по возрастанию (чтобы исключить ошибки с лишними или недостающими перестановками). А затем аккуратно считаем перестановки либо по формуламPk = k! - перестановки без повторений, Pk1, k2, ..., kn = k!/(k1!·k2!· ...·kn!) - перестановки с повторениями, либо рассуждением.
По формулам: P3 = 3! = 1·2·3 = 6 и P1,2 = 3!/(1!·2!) = 1·2·3/(1·1·2) = 3.
Рассуждением: если 2 числа одинаковые, а 3-е отличается, то оно может стоять на 1-ом, 2-ом или 3-ем местах, получится 3 перестановки, если все 3 числа разные, то каждое из них может стоять на 1-ом месте, а оставшиеся два занимать 2-е и 3-е или 3-е и 2-е места, соответственно, тогда 3·2 = 6 перестановок.
Способ II.
Для этой задачи тоже можно посчитать варианты с помощью таблички, но уже 3-D!
Ответ: 0,07
Решение задач с применением таблиц
задачи 14  и задачи 15
и задачи 15 
способом II - перебором вариантов с использованием таблиц. (Для просмотра щелкните по иконке.)
Постарайтесь рассмотреть эти примеры не только как решение конкретной задачи, но и как иллюстрацию к правилам сложения и умножения исходов испытаний, а также для того, чтобы окончательно определиться с выбором метода решения для экзамена. Как лучше - перебором вариантов или по формулам?
Вывод: задачи по теории вероятности этого задания можно решать по единственной формуле в одно действие, если сумеете подсчитать числа возможных и благоприятствующих событий "на пальцах", схемах, таблицах... Однако, чем сложнее эксперимент ("... монету бросают четырежды ...", "... бросают три игральные кости ..."), тем более громоздко "простое" решение и тем короче "сложное" - с использованием формул, правил и теорем.
Рекомендую почитать:
· Лютикас В.С. Школьнику о теории вероятностей. - М. "Просвещение", 1976.
· Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. Пер. с англ. - М. "Наука", 1985.
Источник: http://mathematichka.ru/ege/problems/problem_B10P1.html








