30 Линеаризовать нелинейную модель
- 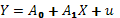 , где
, где 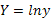 ,
, 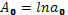 ,
, 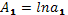 ,
, 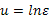
- 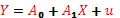 , где
, где 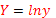 ,
, 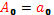 ,
, 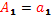 ,
, 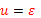
- 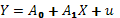 , где
, где 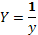 ,
, 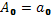 ,
, 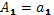 ,
, 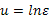
- 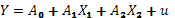 , где
, где 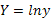 ,
, 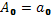 ,
, 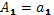 ,
, 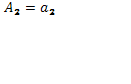 ,
, 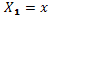
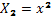
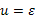
31. Линеаризовать нелинейную модель 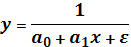
- 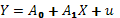 , где
, где 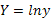 ,
, 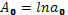 ,
, 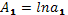 ,
, 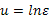
- 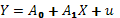 , где
, где 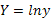 ,
, 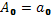 ,
, 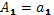 ,
, 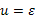
- 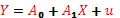 , где
, где 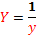 ,
, 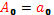 ,
, 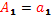 ,
, 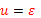
- 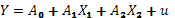 , где
, где 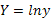 ,
, 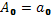 ,
, 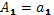 ,
, 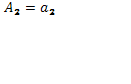 ,
, 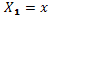
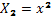
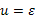
32. Линеаризовать нелинейную модель 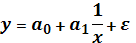
- 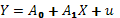 , где
, где 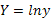 ,
, 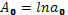 ,
, 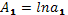 ,
, 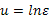
- 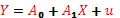 , где
, где 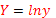 ,
, 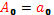 ,
, 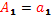 ,
, 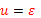
- 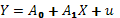 , где
, где 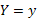 ,
, 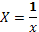
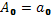 ,
, 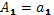 ,
, 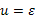
- 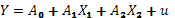 , где
, где 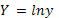 ,
, 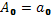 ,
, 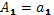 ,
, 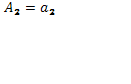 ,
, 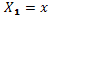
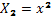
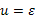
33.Линеаризовать нелинейную модель 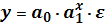
- 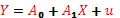 , где
, где 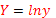 ,
, 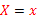 ,
, 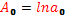 ,
, 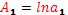 ,
, 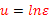
- 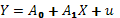 , где
, где 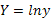 ,
, 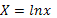 ,
, 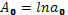 ,
, 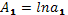 ,
, 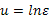
- 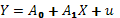 , где
, где 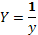 ,
, 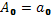 ,
, 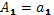 ,
, 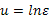
- 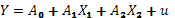 , где
, где 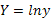 ,
, 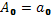 ,
, 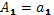 ,
, 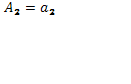 ,
, 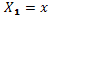
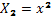
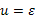
34.Линеаризовать нелинейную модель 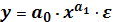
- 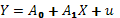 , где
, где 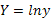 ,
, 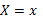 ,
, 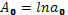 ,
, 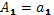 ,
, 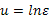
- 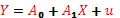 , где
, где 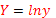 ,
, 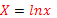 ,
, 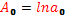 ,
, 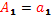 ,
, 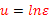
- 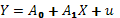 , где
, где 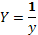 ,
, 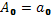 ,
, 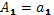 ,
, 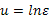
- 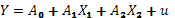 , где
, где 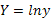 ,
, 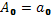 ,
, 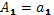 ,
, 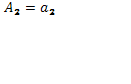 ,
, 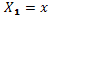
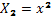
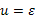
35.Линеаризовать нелинейную модель 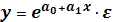
- 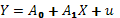 , где
, где 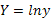 ,
, 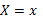 ,
, 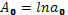 ,
, 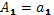 ,
, 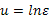
- 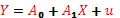 , где
, где 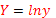 ,
, 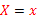 ,
, 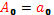 ,
, 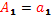 ,
, 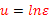
- 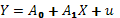 , где
, где 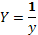 ,
, 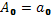 ,
, 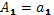 ,
, 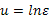
- 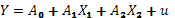 , где
, где 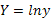 ,
, 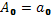 ,
, 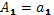 ,
, 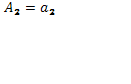 ,
, 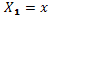
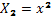
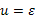
36.Линеаризация экспоненциальной зависимости Y = a 0 ⋅ Xa 1 ⋅ ε (кривой Энгеля, отражающей зависимость спроса от уровня семейных доходов) основана на ...
- интегрировании функции по параметрам
- дифференцировании функции по параметрам
- разложении функции в ряд
- логарифмировании и замене преобразованной переменной
37.Относительные отклонения расчётных значений результирующего признака от его наблюдаемых значений используются при расчёте ...
- t-критерия Стьюдента
- параметров регрессии
- коэффициента эластичности
- средней ошибки аппроксимации
38. Найдите предположение, не являющееся предпосылкой классической модели
Случайные ошибки имеют нулевые математические ожидания.
- Случайные ошибки имеют постоянную дисперсию.
- Случайные ошибки не зависят от объясняющих переменных.
- Случайные ошибки не имеют нормального распределения.
39.Суть коэффициента детерминации состоит в следующем:
- свидетельствует о значимости коэффициентов регрессии
- показывает насколько лучше рассматриваемая модель регрессии по сравнению с тривиальной моделью
- свидетельствует о наличии (отсутствии) автокорреляции
- является мерой сравнения качества любых двух регрессионных моделей
40. Какое значение может принимать коэффициент детерминации:
- 0,4
- –0,5
- –1,2
- 1,1
41. Согласно содержанию регрессии, наблюдаемая величина зависимой (объясняемой) переменной складывается из:
- теоретического значения зависимой переменной, найденного из уравнения регрессии, и случайного отклонения
- теоретического значения зависимой переменной, найденного из уравнения регрессии, скорректированного на величину стандартной ошибки
- теоретического значения зависимой переменной, найденного из уравнения регрессии и остаточной дисперсии
42. С увеличением числа наблюдений дисперсии МНК-оценок неизвестных параметров в модели регрессии:
- уменьшаются
- увеличиваются
- не изменяются
43. С увеличением объема выборки:
- увеличивается точность оценок
- увеличивается точность прогноза, построенного на основании модели
- уменьшается коэффициент детерминации
- оценки становятся не состоятельными
44. По формуле 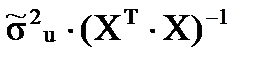 вычисляется
вычисляется
- оценка ковариационной матрицы оценок коэффициентов модели;
- дисперсия экзогенных переменных;
- дисперсия случайного возмущения;
- оценка дисперсии эндогенных переменных модели.
45. По формуле 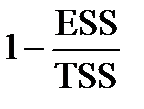 вычисляется
вычисляется
- F – тест;
- статистика критерия Дарбина-Уотсона;
- коэффициент детерминации;
- статистика критерия Голдфелда-Квандта.








