Основные понятия комбинаторики
В разделе математики, который называется комбинаторикой, решаются задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств
Например,возьмём 10 различных цифр 0,1,2,3,…….9 и составим из них комбинации различных чисел : 345, 23, 32, 5036, 1248
Назовите комбинации, которые отличаются
--порядком
--числом цифр
--входящими в них цифрами
Таким образом, полученные комбинации удовлетворяют различным условиям. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания. Рассмотрим их отдельно. Предварительно познакомимся с понятием факториала.
1. Понятие факториала
Определение. Произведение всех натуральных чисел от 1 до п
включительно называют n- Факториалом и пишут
n ! = 1 • 2 • 3 • 4 •... • ( n -1) • n
Считают,что 1!=1; 0!=1
ПРИМЕРЫ :
Вычислить :
3! = 1* 2*3=6
8!= 5!*6*7*8 =6!*7*8
7!- 5! = 5!*6*7 – 5! = 5! (6*7-1)= 1*2*3*4*5*(41)=120*41=4920
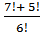= (5!*6*7 + 5!) / 5!*6 = 5! (6*7+1) / 5!*6 =43/6
Вычилить:
, 
, 
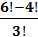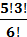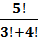
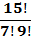
2.Перестановки
Пример: Пусть даны три буквы А, В, С.
Составим всевозможные комбинации из этих букв.(например АВС )
Определение Комбинации из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.
Перестановки обозначаются символом Р n, где n - число элементов, входящих в каждую перестановку
Число перестановок можно вычислить по формуле
Р n = n !
Пример: Сколько различных пятизначных чисел можно составить из цифр 1,2,3,4,5 при условии, что ни одна цифра в числе не повторяется?
3. Размещения
Пример :Пусть имеются четыре буквы A, B, C, D.
Составить комбинации только из двух букв.(например АВ, ВА )
Определение Комбинации из m элементов по n элементов, которые отличаются друг от друга или самими элементами, или порядком элементов, называются размещениями.
Размещения обозначаются символом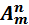 
,
где m- это число всех имеющихся элементов,
n- число элементов в каждой комбинации, (m≥n),
и вычисляются по формуле
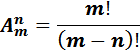
Пример: Сколько двузначных чисел можно составить из пяти цифр 1,2,3,4,5 при условии, что ни одна из них не повторяется.
4 .Сочетания
Пример: Из четырех различных букв A, B, C, D
составить комбинации, которые отличающиеся друг от друга хотя бы одним элементом (например АВ,ВС)
Определение. Сочетаниями называют все комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним элементом, (n≤m).
Сочетания обозначаются символом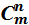 
и вычисляются по формуле
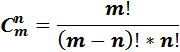
Пример: В ящике имеется 10 деталей. Сколькими способами можно выбрать две детали из этого ящика