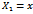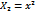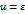10.Величина коэффициента эластичности показывает …
Регрессионная модель с одной объясняющей переменной
1. Парный линейный коэффициент корреляции характеризует наличие тесной обратной связи. Он может принимать следующие значения:
- –0,82;
2. Коэффициент уравнения парной регрессии показывает:
- на сколько единиц изменится зависимая переменная, если независимая переменная изменится на 1 ед.
3. Факторная дисперсия вычисляется по формуле:
- 
;
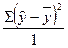4. Коэффициент детерминации показывает:
- на сколько процентов изменение зависимой переменной зависит от изменения независимой переменной;
-
5.Дисперсионный анализ уравнения парной регрессии проверяет:
- значимость уравнения регрессии;
6. Что минимизируется согласно методу наименьших квадратов:
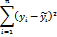
7. Дана ковариационная матрица вектора оценок коэффициентов регрессии:
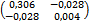
Чему равна несмещенная оценка дисперсии элемента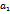 
:
- 0,306;
- 0,004;
- 0,152;
- -0,028.
8. Дана ковариационная матрица вектора оценок коэффициентов регрессии:
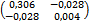
Чему равна несмещенная оценка дисперсии элемента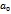 
:
- 0,306;
- 0,004;
- 0,152;
- -0,028.
9.В линейной регрессии Y=b0+b1X+e параметрами уравнения регрессии являются:
- b0;
- b1 .
10.Величина коэффициента эластичности показывает …
- на сколько процентов изменится в среднем результат при изменении фактора на 1% ;
11.Коэффициент корреляции, равный нулю, означает, что между переменными
- линейная связь отсутствует,
12.Коэффициент регрессии изменяется в пределах от
- принимает любое значение.
13.В каких пределах изменяется коэффициент детерминации
- от 0 до 1,
14.Неправильный выбор функциональной формы или объясняющих переменных называется
- ошибками спецификации,
15.Величина, рассчитанная по формуле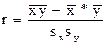 
является оценкой
- парного коэффициента корреляции,
16.Выборочный коэффициент корреляции r по абсолютной величине
- не превосходит единицы,
17.Если в уравнении регрессии имеется несущественная переменная, то она обнаруживает себя по низкому значению
- t – статистики,
18.В каком случае модель считается адекватной?
- 
,
-
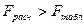19.Как интерпретируется в линейной модели коэффициент регрессии b 1 ?
- коэффициент абсолютного роста.
20.Как в показательной модели интерпретируется коэффициент регрессии b 1 ?
- коэффициент относительного роста,
21.Как в степенной модели интерпретируется коэффициент регрессии b 1 ?
- коэффициент эластичности,
22.Применим ли метод наименьших квадратов для расчёта параметров нелинейных моделей?
- применим после её специального приведения к линейному виду.
23.Что показывает коэффициент регрессии показательной модели?
- на сколько процентов изменится y , если x изменился на один процент,
24.Какую модель следует выбрать, если есть основания считать, что в изучаемом периоде коэффициент относительного роста не изменяется?
- показательную,
- степенную.
25.Какую модель следует выбрать, если есть основания считать, что в изучаемом периоде коэффициент эластичности не изменяется?
- показательную,
26.Если коэффициент корреляции положителен, то в линейной модели
- с ростом х увеличивается у,
27.Если коэффициент корреляции отрицателен, то в линейной модели
- с ростом х уменьшается у,
28.С помощью какого критерия оценивается значимость коэффициентов регрессии?
- t-Стьюдента.
29.Линеаризовать нелинейную модель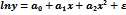 
- 
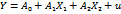, где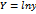 
, 
, 
, 
, 
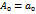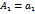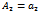