Показательные неравенства
Пример.
Решить двойное неравенство 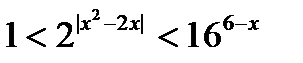 .
.
Решение.
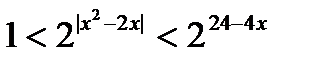 ;
;
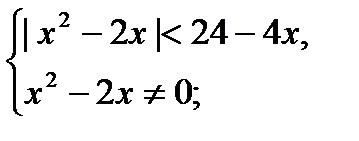
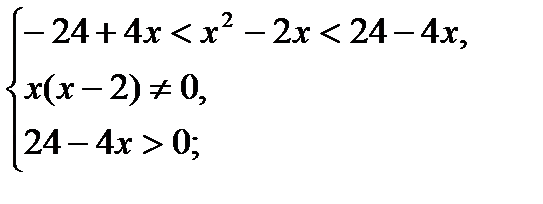
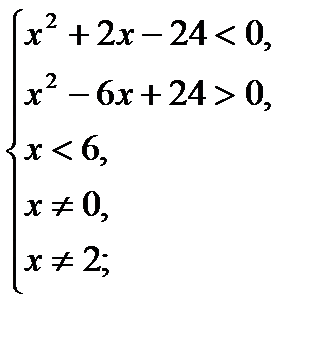
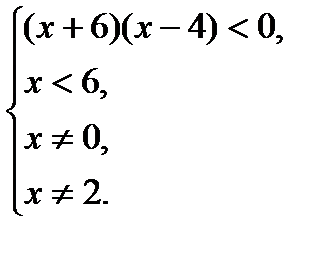
Ответ: 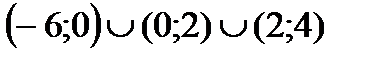 .
. 
Для самостоятельного решения
Решить неравенства:
1) ( 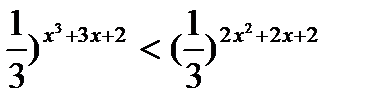 ;
;
2) 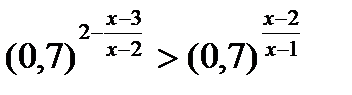 ;
;
3) 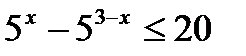 ;
;
4) 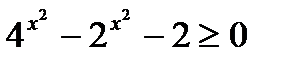 ;
;
5) 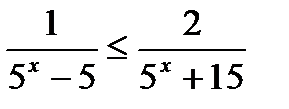 ;
;
6) 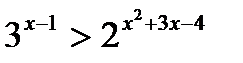 ;
;
7) 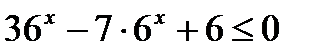 ;
;
8) 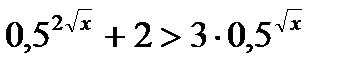 ;
;
9) 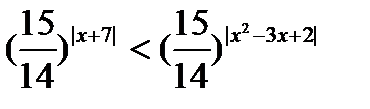 ;
;
10)
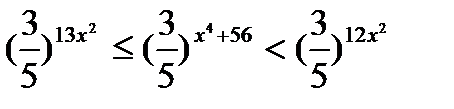 .
.
Логарифмические неравенства
Пример.
Решить неравенство: log2(9 – 2x) ≥ 3log3(3-x).
Решение.
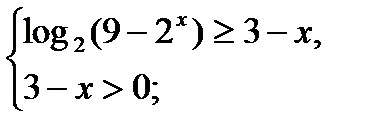
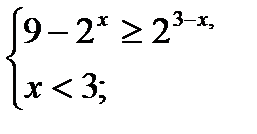
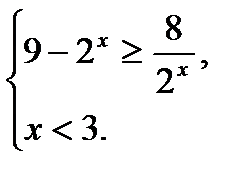
Т.к. 2х> 0 при всех действительных значениях х, то, умножив первое неравенство системы на 2х, получим:
9 . 2х – 22х ≥ 8;
22х – 9 . 2х + 8 ≤ 0;
(2х – 1)(2х – 8) ≤ 0;
1 ≤ 2х ≤ 8.
Т.о., имеем 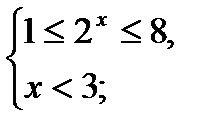
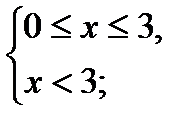
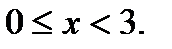
Ответ: 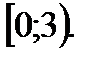
Для самостоятельного решения
1. Решить неравенства:
1) xlog3x ≥ 81;
2) 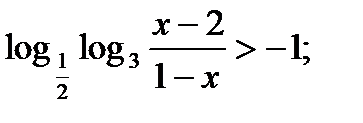
3) 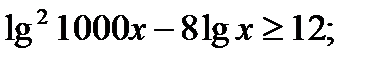
4) logx(2x + 3) < 2;
5) 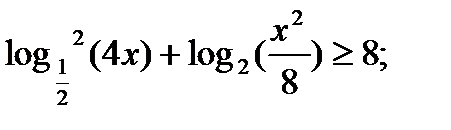
2. Найти область определения функции 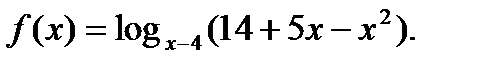
Тригонометрические неравенства
Пример.
Решить неравенство: 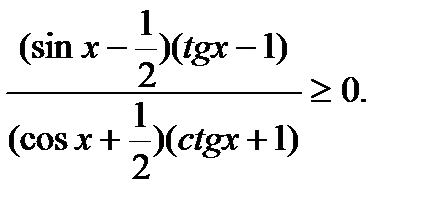
Решение.
Общий период функции, которая находится в левой части неравенства,
Т = 2П. Нули знаменателя:
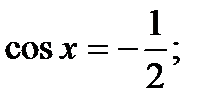
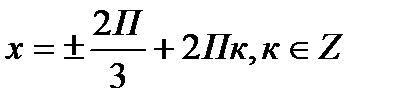 ;
;
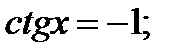
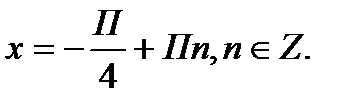
Нули числителя: 
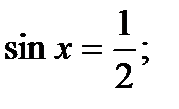
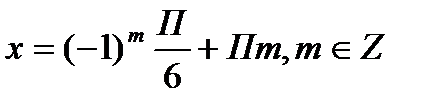 ;
;
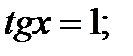
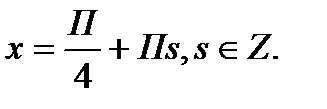
Кроме того 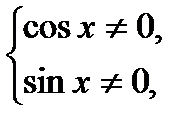
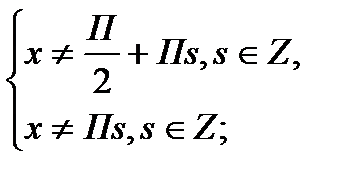
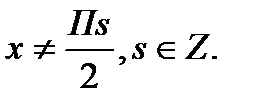
Обозначим на промежутке 
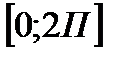 все корни знаменателя («светлые точки») и числителя («тёмные точки») и обозначим знаки функции на полученных промежутках.
все корни знаменателя («светлые точки») и числителя («тёмные точки») и обозначим знаки функции на полученных промежутках.
+ - + - + - + - + - + -
◦ ▪ ▪ ◦ ◦ ◦ ▪ ◦ ▪ ◦ ◦ ◦ ◦
0 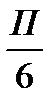
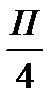
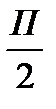
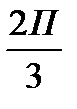
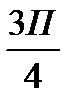
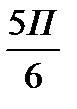 П
П 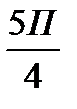
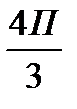
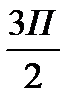
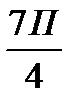 2П
2П
Ответ: 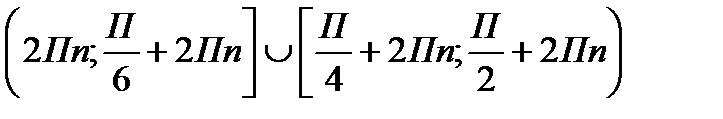
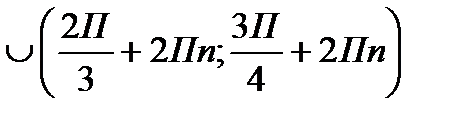

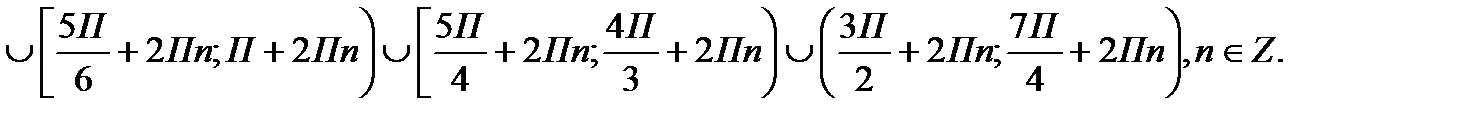
Для самостоятельного решения
Решить неравенства:
1) 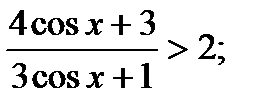
2) sin3x ≥ sinx;
3) tg2x + (2 - 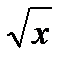 )tgx - 2
)tgx - 2 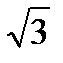 < 0;
< 0;
4) ctg2x + ctgx> 0;
5) tg3x + tg2x > 1 + tgx;
6) 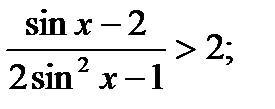
7) 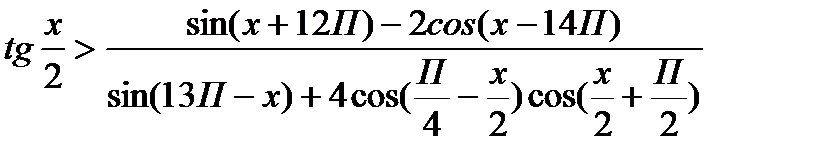 .
.
Комбинированные неравенства
Пример. Решить неравенство: 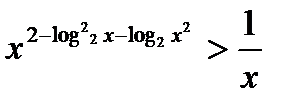 .
.
Решение: 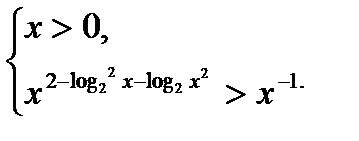
1) х = 1 не является решением неравенства;
2) 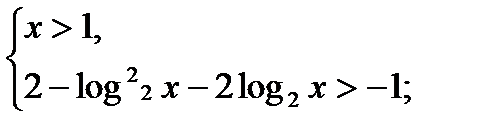
+ - +
◦ ◦ t
-3 1
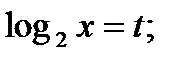
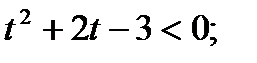 -3 < t < 1;
-3 < t < 1;
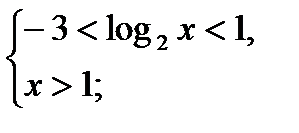
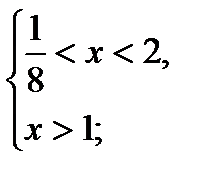
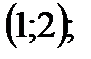
3) 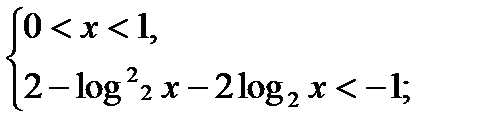
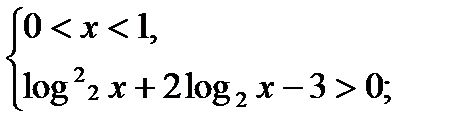
+ - +
◦ ◦ 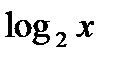
-3 1

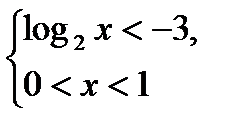 или
или 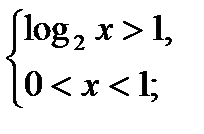
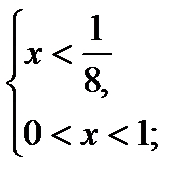
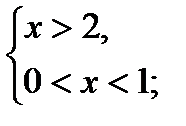
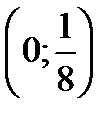 нет решений
нет решений
Ответ: 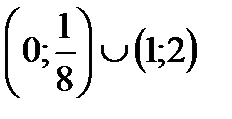 .
.
Для самостоятельного решения
Решить неравенства:
1) 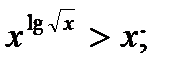
2) 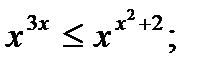
3) 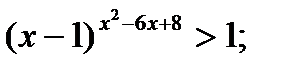
4) 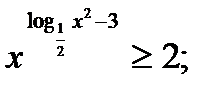
5) 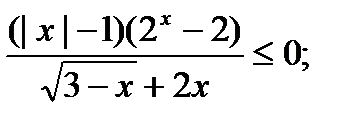
6) 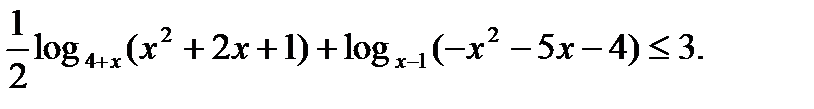
Метод интервалов достаточно универсальный и во многих случаях его применение облегчает решение неравенств, однако это не означает, что все неравенства необходимо решать методом интервалов.

Приложение 2
Тест по теме «Рациональные неравенства»
Вариант 1
1. Решить неравенство 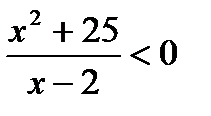
| А | Б | В | Г | Д |
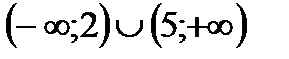
| 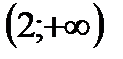
| 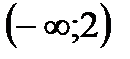
| 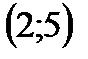
| 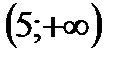
|
2. Решить неравенство 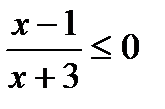
| А | Б | В | Г | Д |
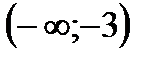
| 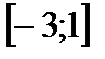
| 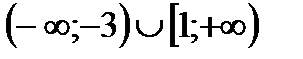
| 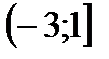
| 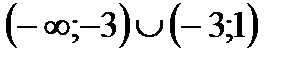
|
3. Решить неравенство 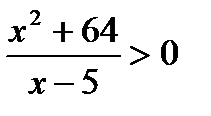
| А | Б | В | Г | Д |
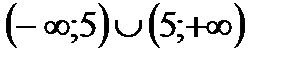
| 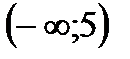
| 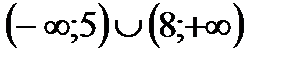
| 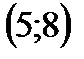
| 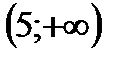
|
4. Решить неравенство 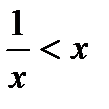
| А | Б | В | Г | Д |
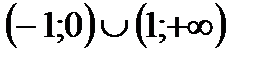
| (-1;0) | 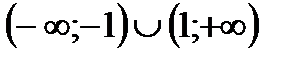
| (-1;1) | 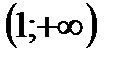
|
5. Решить неравенство 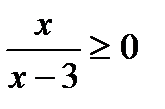
| А | Б | В | Г | Г |
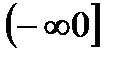
| 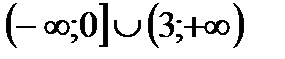
| 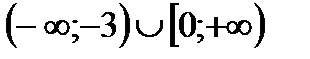
| 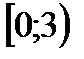
| 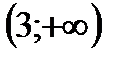
|
6. Решить неравенство 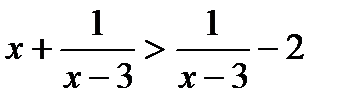
| А | Б | В | Г | Д |
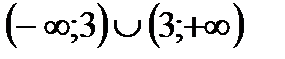
| 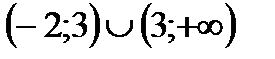
| 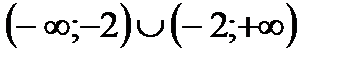
| (2;3) | 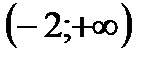
|
7. Найти область определения функции 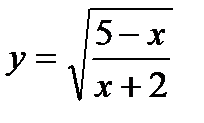
| А | Б | В | Г | Д |
| (-2;5) | 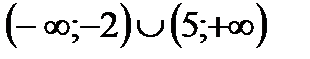
| 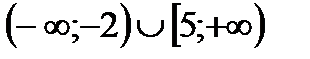
| 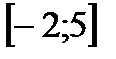
| 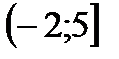
|
8. Указать целое число решений неравенства 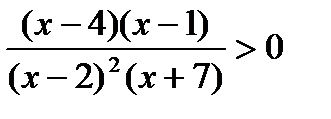 на промежутке
на промежутке 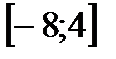 .
.
9. Указать наименьшее целое число, которое является решением неравенства 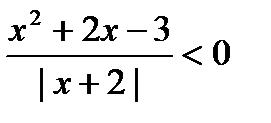 .
.
Вариант 2
1. Решить неравенство 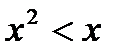
| А | Б | В | Г | Д |
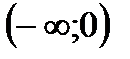
| 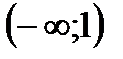
| 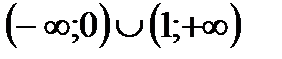
| (0;1) | 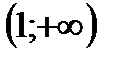
|
2. Решить неравенство 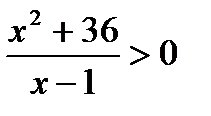
| А | Б | В | Г | Д |
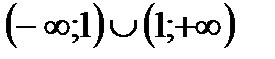
| 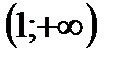
| 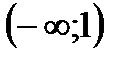
| (1;6) | 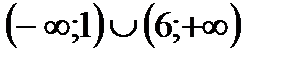
|
3. Решить неравенство 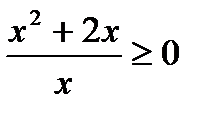
| А | Б | В | Г | Д |
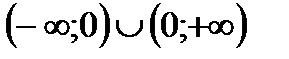
| 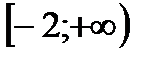
| 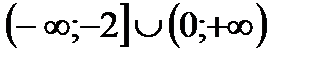
| 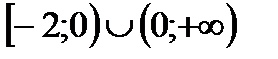
| 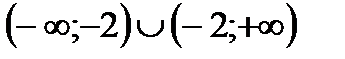
|
4. Решить неравенство 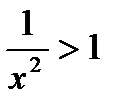
| А | Б | В | Г | Д |
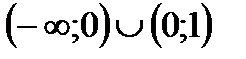
| 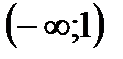
| 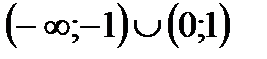
| (-1;1) | 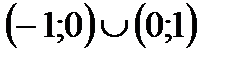
|
5. Решить неравенство 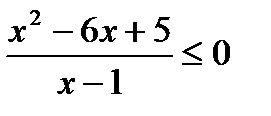
| А | Б | В | Г | Д |
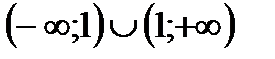
| 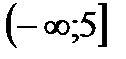
| 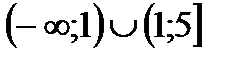 
| 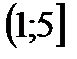
| 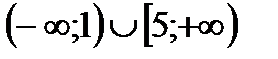
|
6. Решить неравенство 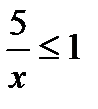
| А | Б | В | Г | Д |
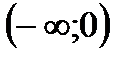
| 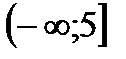
| 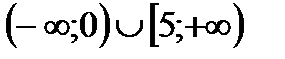
| 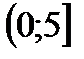
| 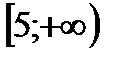
|
7. Найти область определения функции 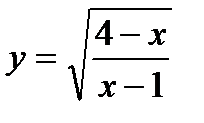
| А | Б | В | Г | Д |
| (1;4) | 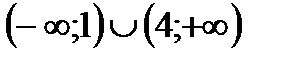
| 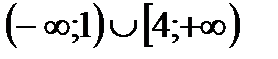
| 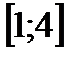
| 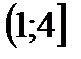
|
8. Указать наименьшее целое число, которое является решением неравенства 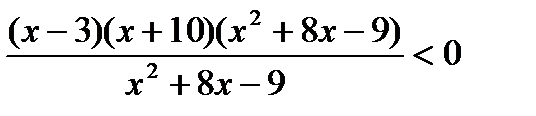 .
.
9. Указать наибольшее целое число, которое является решением неравенства 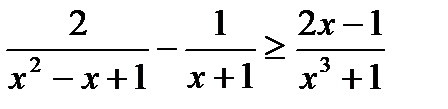 .
.








