Рациональные неравенства

Дата: 2025-06-02; Просмотры: 9

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Пример.

При каких значениях переменной bнеравенство 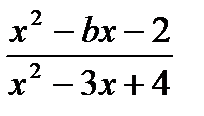> -1 выполняется при всех действительных значениях x?

Решение.

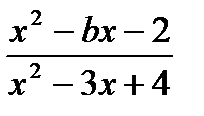+ 1 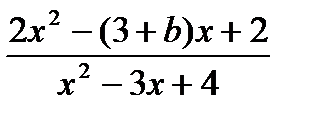> 0; > 0.

Знаменатель неравенства корней не имеет, т.к. х² – 3 + 4х > 0 при всех х 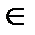R. Следовательно, числитель должен принимать также только положительные значения.

Квадратный трёхчлен с положительным старшим коэффициентом принимает положительные значения при всех действительных значениях переменной, если Д < 0.

Числителем является трёхчлен с положительным старшим коэффициентом, следовательно, его дискриминант

Д = (3 + b)² – 16 < 0;

(3 + b – 4)(3 + b + 4) < 0;

(b – 1)(b + 7) < 0.

+ -7 - 1 +

◦ ◦ b

Ответ: при b .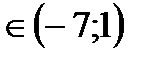

Для самостоятельного решения

1. Решить неравенства:

1) < ;

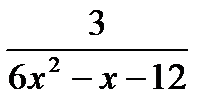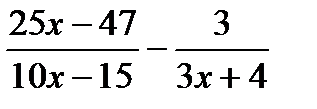2) ;

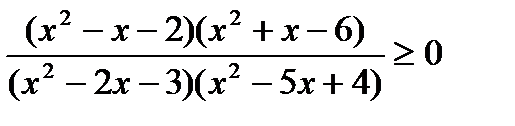3) ;

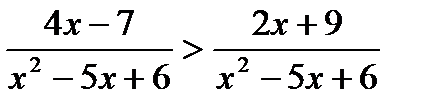4) ;

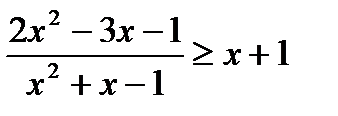5) 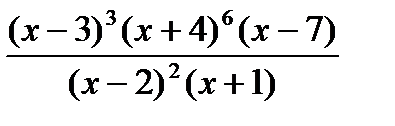≤ 0;

6) ;

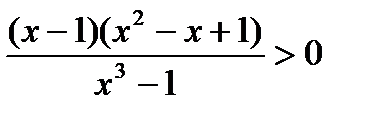7) ;

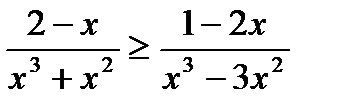8) ;

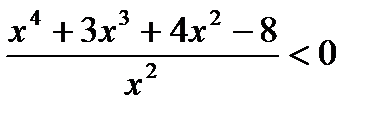9) (x² -3x + 1)² + 3(x – 1)(x² – 3x + 1) ≥ 4(x – 1)²;

2. Найти область определения функции

у = ;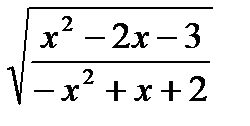

3. Найти промежутки возрастания и убывания, экстремумы функции

у = .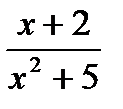

Неравенства, содержащие знак модуля

Пример.

Решить неравенство: ||2x + 1| - |x – 1|| ≤ x + 2.

Решение.

ОДЗ: х ≥ -2.

2х + 1 - + +

х – 1 - - +

х

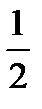-2 - 1

Составим совокупность трёх систем неравенств:

1)

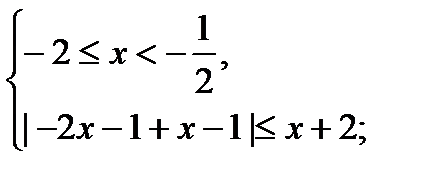
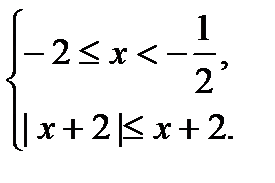
Т.к. |-x-2| = |x + 2| иx + 2 ≥ 0, то |x + 2| = x + 2, т.е. то второе неравенство системы выполняется, поэтому решение системы .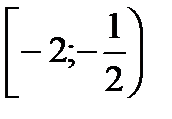

2)

;

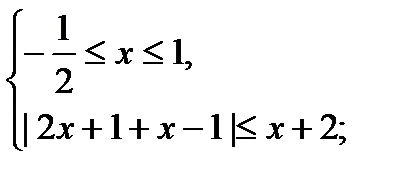
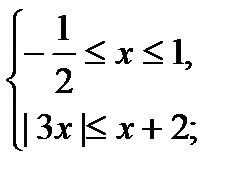
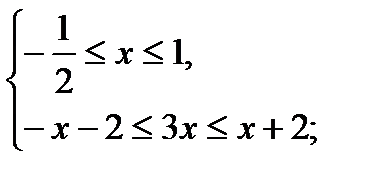
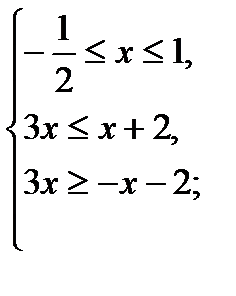
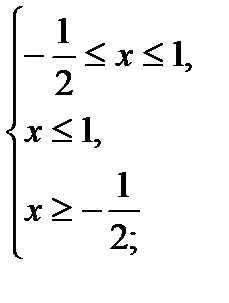
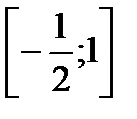3) 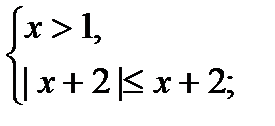х> 1; .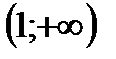

Ответ: .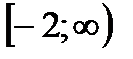

Для самостоятельного решения

1. Решить неравенство:

1) ||2x – 1| - 3| > 2;

2) (|x| - 1)²> 2;

3) |x² – 4|x| + 3| < 1;

4) |x² - 5x| ≤ x + 3;

5) |x² – 3x| ≥ x + 2;

6) |2x² – x – 1| ≥ |x² – 3x – 1|;

7) ;

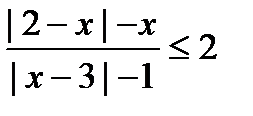8) |x³ – 3x + 1| ≤ x³ + x² – 1;

9) |- ;

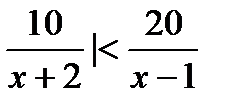10) |x-1|+|x-2|≥ 1;

11) 2|x-1| ≤ x + 3;

12) x² - |5x – 3| - x < 2;

13) ;

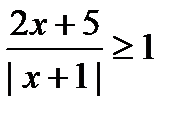14) 3|x – 2| + |5x + 4| ≤ 10;

15) ;

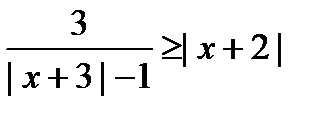16)

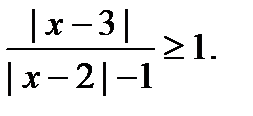
Иррациональные неравенства

Пример.

Для каждого значения a решить неравенство а .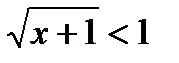

Решение.

1) Если а = 0, то х + 1 ≥ 0, т.е. х ≥ -1.

2) Если а > 0, то .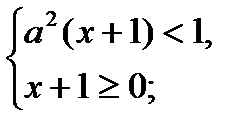

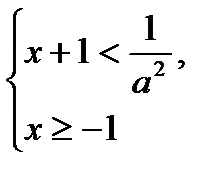
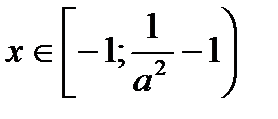3) Если a < 0, то х ≥ -1.

Ответ: 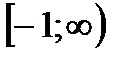, если а ≤ 0; 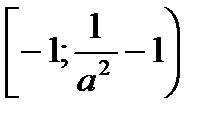, если а> 0.

Для самостоятельного решения

1. Решить неравенства:

1) ;

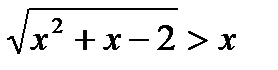2) ;

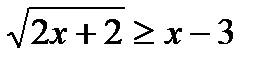3) х + 2 < ;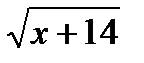

4) x+4 < ;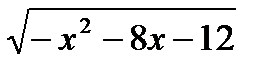

5) ;

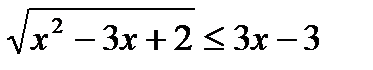6) ;

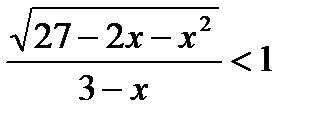7) 8 + 6|3 - ;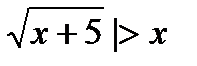

8) ;

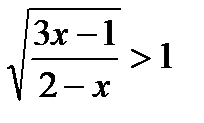9) x ;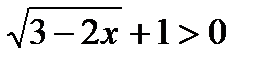

10) ;

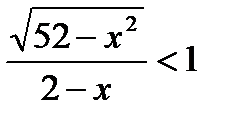11) ;

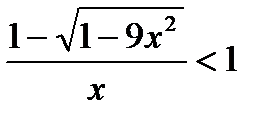12) ;

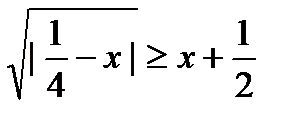13) ;

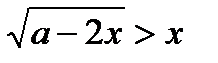14) x + 4a ≥ 5 .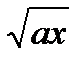

2. Найти область определения функции y= 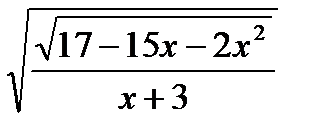.