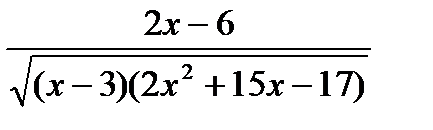Учебно – тематический план
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУК
ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ДОНЕЦКИЙРЕСПУБЛИКАНСКИЙ ИНСТИТУТ
ДОПОЛНИТЕЛЬНОГО ПЕДАГОГИЧЕСКОГО ОБРАЗОВАНИЯ
Отдел образованияадминистрации города Тореза
Общеобразовательная школаI-III ступеней №8 им.Д.А.Рыбалко г.Тореза
СОГЛАСОВАНО
Донецкий Республиканский институт
дополнительного педагогического
образования
Протокол заседания Учёного совета
от____________2016г. № ______
УТВЕРЖДЕНО
Министерство образования и науки
Донецкой Народной Республики
Донецкой Народной Республики
Приказ от_________2016 г. №_____
Программафакультативного курса
РЕШЕНИЕ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ
11класс общеобразовательной школы
18 часов
Автор (составитель)
Смульская Алла Ивановна,
учитель математики, специалист
высшей категории, старший учитель
Общеобразовательной школы
I-III ступеней № 8 г. Тореза
Донецк – 2016
«Одобрено к использованию в образовательных организациях»
Министерство образования и науки ДНР
Приказ от_________________№ _________
Рецензенты:
1. Карташова Валентина Васильевна, учитель математики, специалист высшей категории, старший учитель общеобразовательной школы I-III ступеней №8 им. Д.А.Рыбалког. Тореза
2. Шамдан Наталья Анатольевна, учитель математики, специалист высшей
категории, старший учитель лицея «Спектр» г. Тореза
Составитель:
Смульская Алла Ивановна, учитель математики, специалист высшей категории, старший учитель Общеобразовательной школы I-III ступеней №8 им. Д.А.Рыбалко г. Тореза
Программа составлена с целью развития, дополнения, углубления содержания базового курса математики, удовлетворения познавательных интересов школьников, развития различных сторон математического мышления, воспитания мировоззрения и личностных качеств средствами углублённого изучения математики.
Автор (составитель) Смульская Алла Ивановна, учитель математики,
специалист высшей категории, старший учитель
Общеобразовательной школы I-III ступеней № 8
им. Д.А. Рыбалко г. Тореза
Рецензенты:
1. Карташова Валентина Васильевна, учитель математики, специалист высшей категории, старший учительОбщеобразовательной школы I-III ступеней №8 им. Д.А.Рыбалко г. Тореза
2. Шамдан Наталья Анатольевна, учитель математики, специалист высшей категории,старший учитель лицея «Спектр» г. Тореза
Утверждено педагогическим советом школы
(протокол от15 декабря 2015г. № 12)
Директор Созанская Е.Н.
Согласовано с методическим центром г.Тореза
Директор Пашкевич Л.И.
Научно-методическая экспертиза ДРИДПО:
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Пояснительная записка
Математическое образование в системе основного общего образования занимает одно из ведущих мест, что объясняется практической значимостью математики, её возможностями в развитии и формировании мышления человека, её вкладом в создание представлений личности о научных методах познания действительности.
Актуальным остаётся вопрос развития, дополнения, углубления содержания базового и профильного курсов математики, удовлетворение познавательных интересов школьников, развитие различных сторон математического мышления, формирование личностных качеств средствами углублённого изучения математики.
Решение неравенств – основной составляющий элемент усвоения обучающимися системы математических знаний. Школьный курс математики предполагает изучение неравенств при решении уравнений, задач, исследовании функций, изучении производной и т.п.
Программа факультативного курса «Решение неравенств методом интервалов» раскрывает содержание одного из основных методов решения неравенств – метода интервалов. Решение неравенств методом интервалов способствует развитию логического мышления, памяти, формированию УУД в процессе работы с заданиями более высокого уровня сложности, воспитанию информационной культуры обучающихся.
Программа разработана в соответствии с Государственным образовательным стандартом основного общего образования Донецкой Народной Республики, стандартом государственной услуги «Предоставление дополнительного образования для детей».
Предназначена для 11 классов общеобразовательной школы.
Цели данного курса:
· углубление и расширение знаний по предмету;
· создание условий для самореализации обучающихся в процессе учебной деятельности;
· развитие интеллектуальных, метапредметных способностей обучающихся.
Для достижения поставленных целей в процессе обучения решаются следующие задачи:
· приобщение обучающихся к работе с учебной литературой,
Internet-ресурсами;
· овладение приёмами когнитивного мышления;
· обеспечение диалогического процесса обучения математике.
Курс предназначен для обучающихся11 класса и рассчитан на 18 часов.
Программа построена на принципах последовательности, системности,
вариативности.
Количество часов, отведённых на изучение тем, является ориентировочным и может корректироваться учителем.
Курс предусматривает проведение как традиционных, так и нестандартных форм обучения: проект, защита исследовательских работ, урок-презентация и т.д.
Основными приёмами оценивания при изучении курса могут быть самоанализ, самооценка учебно-познавательной деятельности, которые направлены на формирование положительной мотивации к учебной деятельности.
Требования к уровню подготовки обучающихся
Программа обеспечивает достижение следующих результатов:
предметные:
· знать основную идею метода интервалов;
· решать все виды неравенств методом интервалов;
· составлять неравенства по условию задач;
· изображать на координатной прямой множество решения неравенства;
· уметь использовать приобретённые знания и умения в практической деятельности для построения и исследования простейших математических моделей;
личностные:
· формировать мировоззрение, соответствующее современному уровню развития науки;
· формировать коммуникативную компетентность в учебно-исследовательской, творческой и других видах деятельности;
· понимать смысл поставленной задачи, выстраивать аргументацию;
· критически и креативно мыслить;
· контролировать процесс и результат учебной деятельности;
метапредметные:
· умение планировать пути достижения целей и способы решения поставленных задач;
· осознанное владение когнитивными процессами;
· умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.
Учебно – тематический план
| № |
Наименование темы | Количество часов | Индивидуальная, самостоятельная деятельность обучающихся | Формы контроля | ||
| всего | теор. занят. | практ. занят. | ||||
| 1. | Теоретические основы метода | 1 | 1 | фронт. опрос | ||
| 2. | Целые неравенства | 1 | 1 | тест | ||
| 3,4 | Рациональные неравенства | 2 | 0,5 | 1,5 | тест | |
| 5,6 | Решение неравенств, содержащих знак модуля | 2 | 0,5 | 1,5 | «страница в Википедии» | индивид. опрос |
| 7,8 | Иррациональные неравенства | 2 | 0,5 | 1,5 | защита проектов | защита проектов |
| 9, 10 | Показательные неравенства | 2 | 0,5 | 1,5 | кейс заданий | самост. работа |
| 11,12 | Логарифмические неравенства | 2 | 0,5 | 1,5 | презентация | индивид. опрос |
| 13,14 | Тригонометрические неравенства | 2 | 0,5 | 1,5 | кейс заданий | самост. работа |
| 15, 16 | Смешанные неравенства | 2 | 0,5 | 1,5 | реферат | индивид. опрос |
| 17,18 | Резерв времени | 2 | защита исследоват. проектов | защита проектов | ||
| Всего | 18 | 4,5 | 13,5 | |||
Программа факультативного курса
«Решение неравенств методом интервалов»
| № | Название темы | Содержание учебного материала | Кол. часов | Планируемые результаты |
| 1 | Теоретические основы метода | Теорема, выражающая основу метода. Алгоритм решения неравенств методом интервалов. Преимущества метода интервалов. | 1 | · знать теорему, выражающую основу метода интервалов; · знать алгоритм решения неравенств методом интервалов; · определение точек чётной и нечётной кратности; · уметь осуществлять выбор правильного ответа |
| 2 | Целые неравенства | Определение целого рационального неравенства. Основные методы разложения на множители. Теорема Безу. Схема Горнера. | 1 | · уметь раскладывать многочлен на множители; · уметь решать целые неравенства |
| 3 | Рациональные неравенства | Определение дробного рационального неравенства. Алгоритм решения рациональных неравенств методом интервалов. Решение рациональных неравенств, в том числе с параметром. | 2 | · уметь решать рациональные неравенства |
| 4 | Решение неравенств, содержащих знак модуля | Определение модуля. Некоторые свойства модуля. Построение графиков функций, содержащих знак модуля. Решение неравенств с модулем. | 2 | · уметь использовать свойства модуля; · уметь строить графики функций, содержащие знак модуля; · уметь решать неравенства, содержащие знак модуля |
| 5 | Иррациональные неравенства | Определение иррационального неравенства. Алгоритм решения иррациональных неравенств чётной и нечётной степени. Решение иррациональных неравенств, в том числе с параметром. | 2 | · знать свойства корня n-степени · уметь находить область определения функции; · уметь решать иррациональные неравенства |
| 6 | Показательные неравенства | Определение показательного неравенства. Алгоритм решения показательных неравенств. Решение показательных неравенств, в том числе с параметром. | 2 | · знать свойства показательной функции; · уметь решать показательные неравенства |
| 7 | Логарифмические неравенства | Определение логарифмического неравенства. Алгоритм решения логарифмических неравенств. Решение логарифмических неравенств, в том числе с параметром. | 2 | · знать свойства логарифмической функции; · уметь решать логарифмические неравенства |
| 8 | Тригонометриче- ские неравенства | Определение тригонометрических неравенств. Алгоритм решения тригонометрических неравенств. Решение тригонометрических неравенств, в том числе с параметром. | 2 | · знать свойства тригонометрических функций; · уметь решать тригонометрические неравенства |
| 9 | Комбинированные неравенства | Алгоритм решения неравенств, в которых встречается несколько функций. Решение комбинированных неравенств. | 2 | · находить область определения сложной функции; · уметь решать смешанные неравенства |
| 10 | Резерв времени | Может быть использован на обобщение материала, на защиту индивидуальных проектов | 2 | · уметь организовать сотрудничество на совместную учебную деятельность |
Информационное обеспечение
Литература, использованная при подготовке программы
1. Голубев В.И., Тарасов В.И. Эффективные пути решения неравенств //
Квантор.-1992.,-№10
2. Лукаш О.В., Прес Е.М. Метод інтервалів.- Х.:Вид.група «Основа», 2007
3. Сборник заданий по математике для поступающих во втузы / Под ред. В.И.Сканави. – М.: Высшая школа, 1992.
4. Симонов А.Я. и др. Система тренировочных задач и упражнений по математике.- М.: Просвещение: Владос, 1994.
5. Федченко Л.Я., Литвиненко Г.М. Разноуровневые задания для тематических и итоговых контрольных работ по алгебре и началам анализа в 10-11 классах. – Донецк: «Каштан», 2008.
Ресурсы для учителя и обучающихся
http://mathus.ru/math/metod-intervalov.pdf
http://mat.1september.ru/1998/no39.htm
http://lib.znate.ru/docs/index-167964.html
Приложение 1
Целые неравенства
Пример.
Решить неравенство: х5 - 5х4 + 7х3 - 2х2 + 4х – 8 ≥ 0
Решение.
Найдём корни многочлена, которые находятся в левой части неравенства. Целыми корнями могут числа среди делителей числа -8, т.е. ±1; ±2; ±4; ±8. Понятно, что отрицательных корней многочлен не имеет, потому что при отрицательных значениях переменной х левая часть неравенства также является отрицательной.
| 1 | -5 | 7 | -2 | 4 | -8 | |
| 1 | 1 | -4 | 3 | 1 | 5 | -3 |
х = 1 корнем не является.
| 1 | -5 | 7 | -2 | 4 | -8 | |
| 2 | 1 | -3 | 1 | 0 | 4 | 0 |
х = 2 является корнем многочлена.
(х – 2)(х4 - 3х3 + х2 + 4) ≥ 0.
Свободный член многочлена, находящегося в скобках, 4. Возможные корни: ±1; ±2; ±4.
Можно выяснить, что отрицательные числа и х = 1 не являются корнями многочлена х4 - 3х3 + х2 + 4 могут быть числа 2 или 4.
| 1 | -3 | 1 | 0 | 4 | |
| 2 | 1 | -1 | -1 | -2 | 0 |
(х – 2)2(х3 – х2 – х – 2) ≥ 0
Свободный член многочлена, который находится в скобках, - 2. Поэтому продолжим проверку единственного из возможных целых корней – число 2.
| 1 | -1 | -1 | -2 | |
| 2 | 1 | 1 | 1 | 0 |
Получим: (х – 2)3(х2 + х + 1) ≥ 02
_ +
▪2 х
Ответ: 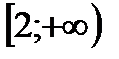 .
.
Задания для самостоятельного решения
1. Решить неравенства:
1) (х + 2)(х2 – х)(3х + 1)(7 – 4х)> 0,
2) (х3- х)(х2-7х +12)(х - 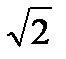 ) ≥ 0;
) ≥ 0;
3) (х2- 5)(1 – х3) ≥0;
4) х4 ≤ 0;
5) (х + 1)(3 – х)(х – 2)2> 0;
6) (х – 7)4(х + 5)5(х – 2)х6(х – 5) > 0;
7) (1 – 2х)2(3х – 9)(4 – 5х)3(х + 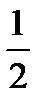 )3(х -
)3(х - 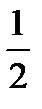 ) < 0;
) < 0;
8) х3 + х2 – х – 1 ≥ 0;
9) (х -4)(х2 + 5х + 7) < (х -4)(2х2 + 4х + 5);
10) (х2 – 2х – 1)(х2 – 2х -3) ≤ 0.
2. Найти область определения функции:
1) у = 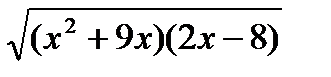 ;
;
2) у =