Математическое ожидание функции одного случайного аргумента.
Пусть Y = φ(X) – функция случайного аргумента Х, и требуется найти ее математическое ожидание, зная закон распределения Х.
1)Если Х – дискретная случайная величина, то
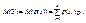 (10.2)
(10.2)
2)Если Х – непрерывная случайная величина, то M(Y) можно искать по-разному. Если известна плотность распределения g(y), то
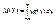
Если же g(y) найти сложно, то можно использовать известную плотность распределения f(x):
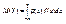
В частности, если все значения Х принадлежат промежутку (а, b), то
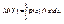
22. Элементы математической статистики. Основные задачи математической статистики.
Математическая статистика занимается установлением закономерностей, которым подчинены массовые случайные явления, на основе обработки статистических данных, полученных в результате наблюдений. Двумя основными задачами математической статистики являются:
- определение способов сбора и группировки этих статистических данных;
- разработка методов анализа полученных данных в зависимости от целей исследования, к которым относятся:
а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости от других случайных величин и т.д.;
б) проверка статистических гипотез о виде неизвестного распределения или о значениях параметров известного распределения.
Для решения этих задач необходимо выбрать из большой совокупности однородных объектов ограниченное количество объектов, по результатам изучения которых можно сделать прогноз относительно исследуемого признака этих объектов.
23. Генеральная и выборочная совокупность. Способы отбора. Статическая функция распределения. Статические оценки параметров распределения.
Определим основные понятия математической статистики.
Генеральная совокупность – все множество имеющихся объектов.
Выборка – набор объектов, случайно отобранных из генеральной совокупности.
Объем генеральной совокупности N и объем выборки n – число объектов в рассматривае-мой совокупности.
Виды выборки:
Повторная – каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность;
Бесповторная – отобранный объект в генеральную совокупность не возвращается.
Замечание. Для того, чтобы по исследованию выборки можно было сделать выводы о поведе-нии интересующего нас признака генеральной совокупности, нужно, чтобы выборка правиль-но представляла пропорции генеральной совокупности, то есть была репрезентативной (представительной). Учитывая закон больших чисел, можно утверждать, что это условие выполняется, если каждый объект выбран случайно, причем для любого объекта вероятность попасть в выборку одинакова.
Первичная обработка результатов.
Пусть интересующая нас случайная величина Х принимает в выборке значение х1 п1 раз, х2 – п2 раз, …, хк – пк раз, причем 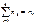 где п – объем выборки. Тогда наблюдаемые значения случайной величины х1, х2,…, хк называют вариантами, а п1, п2,…, пк – частотами. Если разделить каждую частоту на объем выборки, то получим относительные частоты
где п – объем выборки. Тогда наблюдаемые значения случайной величины х1, х2,…, хк называют вариантами, а п1, п2,…, пк – частотами. Если разделить каждую частоту на объем выборки, то получим относительные частоты 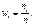 Последовательность вариант, записанных в порядке возрастания, называют вариационным рядом, а перечень вариант и соответствующих им частот или относительных частот – стати-стическим рядом:
Последовательность вариант, записанных в порядке возрастания, называют вариационным рядом, а перечень вариант и соответствующих им частот или относительных частот – стати-стическим рядом:
| xi | x1 | x2 | … | xk |
| ni | n1 | n2 | … | nk |
| wi | w1 | w2 | … | wk |
Если исследуется некоторый непрерывный признак, то вариационный ряд может состоять из очень большого количества чисел. В этом случае удобнее использовать группированную выборку. Для ее получения интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько равных частичных интервалов длиной h, а затем находят для каждого частичного интервала ni – сумму частот вариант, попавших в i-й интервал. Составленная по этим результатам таблица называется группированным статистическим рядом:
| Номера интервалов | 1 | 2 | … | k |
| Границы интервалов | (a, a + h) | (a + h, a + 2h) | … | (b – h, b) |
| Сумма частот вариант, попав- ших в интервал | n1 | n2 | … | nk |
Распределение функции.
Для наглядного представления о поведении исследуемой случайной величины в выборке можно строить различные графики. Один из них – полигон частот: ломаная, отрезки которой соединяют точки с координатами (x1, n1), (x2, n2),…, (xk , nk), где xi откладываются на оси абсцисс, а ni – на оси ординат. Если на оси ординат откладывать не абсолютные (ni), а относительные (wi) частоты, то получим полигон
 рис.1
рис.1
относительных частот (рис.1).
По аналогии с функцией распределения случайной величины можно задать некоторую функцию, относительную частоту события X < x .
Выборочной (эмпирической) функцией распределения называют функцию F *(x), определяющую для каждого значения х относительную частоту события X < x . Таким образом,
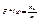 , (15.1)
, (15.1)
где пх – число вариант, меньших х, п – объем выборки.
Замечание. В отличие от эмпирической функции распределения, найденной опытным путем, функцию распределения F(x) генеральной совокупности называют теоретической функцией распределения. F(x) определяет вероятность события X < x, а F *(x) – его относительную частоту. При достаточно больших п, как следует из теоремы Бернулли, F *(x) стремится по вероятности к F(x).
Из определения эмпирической функции распределения видно, что ее свойства совпадают со свойствами F(x), а именно:
1) 0 ≤ F *(x) ≤ 1.
2) F *(x) – неубывающая функция.
3) Если х1 – наименьшая варианта, то F *(x) = 0 при х≤ х1; если хк – наибольшая варианта, то F *(x) = 1 при х > хк .
Для непрерывного признака графической иллюстрацией служит гистограмма, то есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высотами – отрезки длиной ni / h (гистограмма частот) или wi / h (гистограмма относительных частот). В первом случае площадь гистограммы равна объему выборки, во втором – единице  Рис.2.
Рис.2.
24. Доверительный интервал для математического ожидания нормального распределения при известном и неизвестном распределении. Коэффициент Стьюдента.
Построение доверительных интервалов.
1. Доверительный интервал для оценки математического ожидания нормального распределения при известной дисперсии.
Пусть исследуемая случайная величина Х распределена по нормальному закону с известным средним квадратическим σ, и требуется по значению выборочного среднего 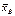 оценить ее математическое ожидание а. Будем рассматривать выборочное среднее
оценить ее математическое ожидание а. Будем рассматривать выборочное среднее 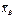 как случайную величину
как случайную величину 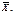 а значения вариант выборки х1, х2,…, хп как одинаково распределенные независимые случайные величины Х1, Х2,…, Хп, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ. При этом М(
а значения вариант выборки х1, х2,…, хп как одинаково распределенные независимые случайные величины Х1, Х2,…, Хп, каждая из которых имеет математическое ожидание а и среднее квадратическое отклонение σ. При этом М( 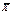 ) = а,
) = а, 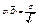 (используем свойства математического ожидания и дисперсии суммы независимых случайных величин). Оценим вероятность выполнения неравенства
(используем свойства математического ожидания и дисперсии суммы независимых случайных величин). Оценим вероятность выполнения неравенства 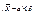 . Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:
. Применим формулу для вероятности попадания нормально распределенной случайной величины в заданный интервал:
р ( 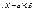 ) = 2Ф
) = 2Ф 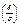 . Тогда , с учетом того, что
. Тогда , с учетом того, что 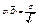 , р (
, р ( 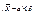 ) = 2Ф
) = 2Ф 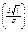 =
=
=2Ф( t ), где 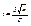 . Отсюда
. Отсюда 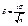 , и предыдущее равенство можно переписать так:
, и предыдущее равенство можно переписать так:
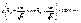 .
.
Итак, значение математического ожидания а с вероятностью (надежностью) γ попадает в интервал 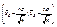 , где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2Ф(t) = γ.
, где значение t определяется из таблиц для функции Лапласа так, чтобы выполнялось равенство 2Ф(t) = γ.
2. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестной дисперсии.
Если известно, что исследуемая случайная величина Х распределена по нормальному закону с неизвестным средним квадратическим отклонением, то для поиска доверительного интервала для ее математического ожидания построим новую случайную величину
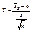 , (18.2)
, (18.2)
где 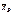 - выборочное среднее, s – исправленная дисперсия, п – объем выборки. Эта случайная величина, возможные значения которой будем обозначать t, имеет распределение Стьюдента (см. лекцию 12) с k = n – 1 степенями свободы.
- выборочное среднее, s – исправленная дисперсия, п – объем выборки. Эта случайная величина, возможные значения которой будем обозначать t, имеет распределение Стьюдента (см. лекцию 12) с k = n – 1 степенями свободы.
Поскольку плотность распределения Стьюдента 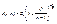 , где
, где 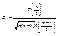 , явным образом не зависит от а и σ, можно задать вероятность ее попадания в некоторый интервал (- tγ , tγ ), учитывая четность плотности распределения, следующим образом:
, явным образом не зависит от а и σ, можно задать вероятность ее попадания в некоторый интервал (- tγ , tγ ), учитывая четность плотности распределения, следующим образом: 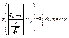 . Отсюда получаем:
. Отсюда получаем: 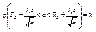 (18.3)
(18.3)
Таким образом, получен доверительный интервал для а, где tγ можно найти по соответствую-щей таблице при заданных п и γ.
26. Элементы теории корреляции. Выборочное уравнение регрессии. Линейная регрессия. Пусть составляющие Х и Y двумерной случайной величины (Х, Y) зависимы. Будем считать, что одну из них можно приближенно представить как линейную функцию другой, например Y ≈ g(Х) = α + β Х, (11.2) и определим параметры α и β с помощью метода наименьших квадратов. Определение 11.2. Функция g(Х) = α + β Х называется наилучшим приближением Y в смысле метода наименьших квадратов, если математическое ожидание М(Y - g(Х))2 принимает наименьшее возможное значение; функцию g(Х) называют среднеквадратической регрессией Y на Х. Теорема 11.1. Линейная средняя квадратическая регрессия Y на Х имеет вид: 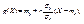 (11.3) где
(11.3) где 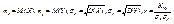 - коэффициент корреляции Х и Y . Доказательство. Рассмотрим функцию F(α , β) = M(Y – α – βX)² (11.4) и преобразуем ее, учитывая соот-ношения M(X – mx) = M(Y – my) = 0, M((X – mx)(Y – my)) = =Kxy = r σ x σ y:
- коэффициент корреляции Х и Y . Доказательство. Рассмотрим функцию F(α , β) = M(Y – α – βX)² (11.4) и преобразуем ее, учитывая соот-ношения M(X – mx) = M(Y – my) = 0, M((X – mx)(Y – my)) = =Kxy = r σ x σ y: 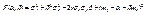 . Найдем стационарные точки полученной функции, решив систему
. Найдем стационарные точки полученной функции, решив систему 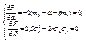
Решением системы будет 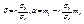 . Можно проверить, что при этих значениях функция F(α, β) имеет минимум, что доказывает утверждение теоремы. Определение 11.3. Коэффициент
. Можно проверить, что при этих значениях функция F(α, β) имеет минимум, что доказывает утверждение теоремы. Определение 11.3. Коэффициент 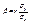 называется коэффициентом регрессии Y на Х, а прямая
называется коэффициентом регрессии Y на Х, а прямая 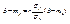 - (11.5) - прямой среднеквадратической регрессии Y на Х.
- (11.5) - прямой среднеквадратической регрессии Y на Х.
Подставив координаты стационарной точки в равенство (11.4), можно найти минимальное значение функции F(α, β), равное 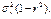 Эта величина называется остаточной дисперсией Y относительно Х и характеризует величину ошибки, допускаемой при замене Y на g(Х) = α + β Х. При
Эта величина называется остаточной дисперсией Y относительно Х и характеризует величину ошибки, допускаемой при замене Y на g(Х) = α + β Х. При 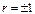 остаточная дисперсия равна 0, то есть равенство (11.2) является не приближенным, а точным. Следовательно, при
остаточная дисперсия равна 0, то есть равенство (11.2) является не приближенным, а точным. Следовательно, при 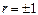 Y и Х связаны линейной функциональной зависимостью. Аналогично можно получить прямую среднеквадратической регрессии Х на Y:
Y и Х связаны линейной функциональной зависимостью. Аналогично можно получить прямую среднеквадратической регрессии Х на Y: 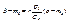 (11.6) и остаточную дисперсию Х относительно Y. При
(11.6) и остаточную дисперсию Х относительно Y. При 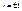 обе прямые регрессии совпадают. Решив систему из уравнений (11.5) и (11.6), можно найти точку пересечения прямых регрессии – точку с координатами (тх, ту), называемую центром совместного распределения величин Х и Y . Линейная корреляция. Для двумерной случайной величины (Х, Y) можно ввести так называемое условное математи-ческое ожидание Y при Х = х. Для дискретной случайной величины оно определяется как
обе прямые регрессии совпадают. Решив систему из уравнений (11.5) и (11.6), можно найти точку пересечения прямых регрессии – точку с координатами (тх, ту), называемую центром совместного распределения величин Х и Y . Линейная корреляция. Для двумерной случайной величины (Х, Y) можно ввести так называемое условное математи-ческое ожидание Y при Х = х. Для дискретной случайной величины оно определяется как 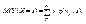 (11.7) для непрерывной случайной величины –
(11.7) для непрерывной случайной величины – 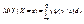 . (11.8) Определение 11.4. Функцией регрессии Y на Х называется условное математическое ожидание M( Y / x ) = f(x). Аналогично определяется условное математическое ожидание Х и функция регрессии Х на Y . Определение 11.5. Если обе функции регрессии Х на Y и Y на Х линейны, то говорят, что Х и Y связаны линейной корреляционной зависимостью. При этом графики линейных функций регрессии являются прямыми линиями, причем можно доказать, что эти линии совпадают с прямыми среднеквадратической регрессии. Теорема .Если двумерная случайная величина (Х, Y) распределена нормально, то Х и Y связаны линейной корреляционной зависимостью. Доказательство. Найдем условный закон распределения Y при Х = х
. (11.8) Определение 11.4. Функцией регрессии Y на Х называется условное математическое ожидание M( Y / x ) = f(x). Аналогично определяется условное математическое ожидание Х и функция регрессии Х на Y . Определение 11.5. Если обе функции регрессии Х на Y и Y на Х линейны, то говорят, что Х и Y связаны линейной корреляционной зависимостью. При этом графики линейных функций регрессии являются прямыми линиями, причем можно доказать, что эти линии совпадают с прямыми среднеквадратической регрессии. Теорема .Если двумерная случайная величина (Х, Y) распределена нормально, то Х и Y связаны линейной корреляционной зависимостью. Доказательство. Найдем условный закон распределения Y при Х = х 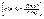 , используя формулу двумерной плотности вероятности нормального распределения (11.1) и формулу плотности вероятности Х:
, используя формулу двумерной плотности вероятности нормального распределения (11.1) и формулу плотности вероятности Х: 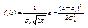 . (11.9) Сделаем замену
. (11.9) Сделаем замену 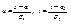 . Тогда
. Тогда 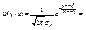
= 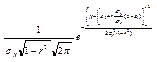 .
.
Полученное распределение является нормальным, а его мате-матическое ожидание 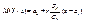 есть функция регрессии Y на Х (см. опреде-ление 11.4)). Аналогично можно получить функцию регрессии Х на Y:
есть функция регрессии Y на Х (см. опреде-ление 11.4)). Аналогично можно получить функцию регрессии Х на Y: 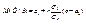 . Обе функции регрессии линейны, поэтому корреляция между Х и Y линейна, что и требовалось доказать. При этом уравнения прямых регрессии имеют вид
. Обе функции регрессии линейны, поэтому корреляция между Х и Y линейна, что и требовалось доказать. При этом уравнения прямых регрессии имеют вид 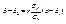 ,
, 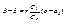 , то есть совпадают с уравнениями прямых среднеквадратической регрессии (см. формулы (11.5), (11.6)).
, то есть совпадают с уравнениями прямых среднеквадратической регрессии (см. формулы (11.5), (11.6)).
29. Метод максимального правдоподобия. Функция правдоподобия в непрерывном и дискретном случаях. Оценка максимального правдоподобия и их основные свойства.
Метод наибольшего правдоподобия.
Пусть Х – дискретная случайная величина, которая в результате п испытаний приняла значения х1, х2, …, хп. Предположим, что нам известен закон распределения этой величины, определяемый параметром Θ, но неизвестно численное значение этого параметра. Найдем его точечную оценку.
Пусть р(х i, Θ) – вероятность того, что в результате испытания величина Х примет значение х i. Назовем функцией правдоподобия дискретной случайной величины Х функцию аргумента Θ, определяемую по формуле:
L (х1, х2, …, хп; Θ) = p(x1,Θ)p(x2,Θ)…p(xn,Θ).
Тогда в качестве точечной оценки параметра Θ принимают такое его значение Θ* = Θ(х1, х2, …, хп), при котором функция правдоподобия достигает максимума. Оценку Θ* называют оценкой наибольшего правдоподобия.
Поскольку функции L и lnL достигают максимума при одном и том же значении Θ, удобнее искать максимум ln L – логарифмической функции правдоподобия. Для этого нужно: 1)найти производную 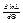 ;
;
2)приравнять ее нулю (получим так называемое уравнение правдоподобия) и найти критическую точку;
3)найти вторую производную 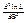 ; если она отрицательна в критической точке, то это – точка максимума.
; если она отрицательна в критической точке, то это – точка максимума.
Достоинства метода наибольшего правдоподобия: полученные оценки состоятельны (хотя могут быть смещенными), распределены асимптотически нормально при больших значениях п и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками; если для оцениваемого параметра Θ существует эффективная оценка Θ*, то уравнение правдоподобия имеет единственное решение Θ*; метод наиболее полно использует данные выборки и поэтому особенно полезен в случае малых выборок.
Недостаток метода наибольшего правдоподобия: сложность вычислений.
Для непрерывной случайной величины с известным видом плотности распределения f(x) и неизвестным параметром Θ функция правдоподобия имеет вид:
L (х1, х2, …, хп; Θ) = f(x1,Θ)f(x2,Θ)…f(xn,Θ).
Оценка наибольшего правдоподобия неизвестного параметра проводится так же, как для дискретной случайной величины.
17. Условные законы распределения. Математическое ожидание и дисперсии я случайных величин. Условное математическое ожидание.
дискретной случайной величины называ-ется сумма произведений ее возможных значений на соответствующие им вероятности:
М(Х) = х1р1 + х2р2 + … + хпрп . (7.1)
Если число возможных значений случайной величины бесконечно, то 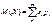
, если полученный ряд сходится абсолютно.
Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.
Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольше-го.
Замечание 3. Математическое ожидание дискретной случайной величины есть неслучай-ная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непре-рывных случайных величин.
Дисперсией (рассеянием) случайной величины называется математи-ческое ожидание квадрата ее отклонения от ее математического ожидания: D(X) = M (X – M(X))²
Замечание 1. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друг друга.
Замечание 2. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения.
Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии, справедливость которой доказывается в следующей теореме:
Теорема. D(X) = M(X ²) – M ²(X).
Доказательство.
Используя то, что М(Х) – постоянная величина, и свойства математического ожидания, преобразуем формулу (7.6) к виду:
D(X) = M(X – M(X))² = M(X² - 2X·M(X) + M²(X)) = M(X²) – 2M(X)·M(X) + M²(X) =
= M(X²) – 2M²(X) + M²(X) = M(X²) – M²(X),
что и требовалось доказать.вв








