Равномерный закон распределения.
Часто на практике мы имеем дело со случайными величинами, распределенными определенным типовым образом, то есть такими, закон распределения которых имеет некоторую стандартную форму. В прошлой лекции были рассмотрены примеры таких законов распределения для дискретных случайных величин (биномиальный и Пуассона). Для непрерывных случайных величин тоже существуют часто встречающиеся виды закона распределения, и в качестве первого из них рассмотрим равномерный закон.
Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение ( f(x) = const при a ≤ x ≤ b , f(x) = 0 при x < a , x > b .
Найдем значение, которое принимает f(x) при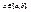 
Из условия нормировки следует, что 
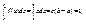откуда 
.
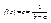Вероятность попадания равномерно распределенной случайной величины на интервал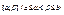 
равна при этом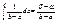 
Вид функции распределения для нормального закона: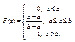 
Числовые характеристики непрерывных случайных величин.
Распространим определения числовых характеристик случайных величин на непре-рывные случайные величины, для которых плотность распределения служит в некото-ром роде аналогом понятия вероятности.
Определение 7.7. Математическим ожиданием непрерывной случайной величины называется
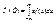Замечание 1.
Общее определение дисперсии сохраняется для непрерывной случайной величины таким же, как и для дискретной
(опр. 7.5), а формула для ее вычисления имеет вид:
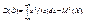
Среднее квадратическое отклонение вычисляется по формуле .
Замечание 2. Если все возможные значения непрерывной случайной величины не выходят за пределы интервала [a , b], то интегралы в формулах (7.13) и (7.14) вычисля-ются в этих пределах.
11.Закон распределения случайных величин. Нормальное распределение. Показательное распределение. Равномерное распределение. Некоторые другие виды распределения.
Непрерывная случайная величина называется распределенной по нормальному закону, если ее плотность распределения имеет вид:
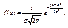(6.1)
Замечание. Таким образом, нормальное распределение определяется двумя параметрами: а и σ.
График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Выясним, какой вид имеет эта кривая, для чего исследуем функцию (6.1).
1)Область определения этой функции: (-∞, +∞).
2) f(x) > 0 при любом х (следовательно, весь график расположен выше оси Ох).
3) 
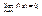то есть ось Ох служит горизонтальной асимптотой графика при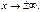 
4) 
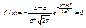при х = а; 
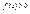при x > a, 
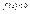при x < a. Следовательно, 
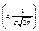- точка максимума.
5) F(x – a) = f(a – x), то есть график симметричен относительно прямой х = а.
6) 
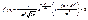при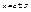 
, то есть точки 
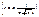являются точками перегиба.
Примерный вид кривой Гаусса изображен на рис.1.
х
Рис.1.
Найдем вид функции распределения для нормального закона:
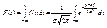(6.2)
Перед нами так называемый «неберущийся» интеграл, который невозможно выразить через элементарные функции. Поэтому для вычисления значений F(x) приходится пользоваться таблицами. Они составлены для случая, когда а = 0, а σ = 1.
Нормальное распределение с параметрами а = 0, σ = 1 называется нормированным, а его функция распределения.