Вероятность появления хотя бы одного события.
Теорема.Вероятность появления хотя бы одного из попарно независимых событий
А1, А2,…, Ап равна р (А) = 1 – q1q2…qn , (2.9)
где qi – вероятность события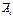 
, противоположного событию А i .
Доказательство.
Если событие А заключается в появлении хотя бы одного события из А1, А2,…, Ап, то события А и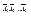 
противоположны, поэтому по теореме 2.2 сумма их вероятностей равна 1. Кроме того, поскольку А1, А2,…, Ап независимы, то независимы и 
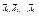, следовательно, р( ) = 
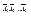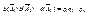. Отсюда следует справедливость формулы (2.9).
5. Формула полной вероятности. Вероятность гипотез. Формула Бейеса.
Пусть событие А может произойти только совместно с одним из событий Н1, Н2,…, Нп, образующих полную группу несовместных событий. Тогда события Н1, Н2,…, Нп называются гипотезами.
Теорема . Вероятность события А, наступающего совместно с гипотезами Н1, Н2,…, Нп, равна:
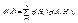(3.1)
где p(Hi) – вероятность i - й гипотезы, а p(A / Hi) – вероятность события А при условии реализации этой гипотезы. Формула (3.1) носит название формулы полной вероятности.
Доказательство.
Можно считать событие А суммой попарно несовместных событий АН1, АН2,…, АНп. Тогда из теорем сложения и умножения следует, что
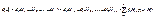
что и требовалось доказать.
Формула Байеса (теорема гипотез)
Пусть известен результат опыта, а именно то, что произошло событие А. Этот факт может изменить априорные (то есть известные до опыта) вероятности гипотез. Например, в предыдущем примере извлечение из урны белого шара говорит о том, что этой урной не могла быть третья, в которой нет белых шаров, то есть р (Н3/А) = 0. Для переоценки вероятностей гипотез при известном результате опыта используется формула Байеса:
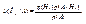(3.2)
Действительно, из (2.7) получим, что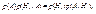 
откуда следует справедливость формулы (3.2).
6. Повторное испытание. Формула Бернулли.
Рассмотрим серию из п испытаний, в каждом из которых событие А появляется с одной и той же вероятностью р, причем результат каждого испытания не зависит от результатов остальных. Подобная постановка задачи называется схемой повторения испытаний. Найдем вероятность того, что в такой серии событие А произойдет ровно к раз (неважно, в какой последовательности). Интересующее нас событие представляет собой сумму равно-вероятных несовместных событий, заключающихся в том, что А произошло в некоторых к испытаниях и не произошло в остальных п – к испытаниях. Число таких событий равно числу сочетаний из п по к, то есть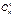 
, а вероятность каждого из них: pkqn - k, где q = 1 – p – вероятность того, что в данном опыте А не произошло. Применяя теорему сложения для несовместных событий, получим формулу Бернулли:
.
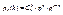Приближение Пуассона для схемы Бернулли.
Формула Бернулли требует громоздких расчетов при большом количестве испытаний. Можно получить более удобную для расчетов приближенную формулу, если при большом числе испытаний вероятность появления А в одном опыте мала, а произведение пр = λ сохраняет постоянное значение для разных серий опытов ( то есть среднее число появле-ний события А в разных сериях испытаний остается неизменным). Применим формулу Бернулли:
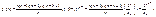
Найдем предел полученного выражения при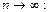 
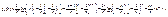
Таким образом, формула Пуассона
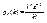
позволяет найти вероятность к появлений события А для массовых (п велико) и редких (р мало) событий.
7. Дискретные случайные величины и их характеристика. Закон распределения вероятностей ДСВ. Математическое ожидание ДСВ. Свойства математического ожидания.
Наряду с понятием случайного события в теории вероятности используется и более удобное понятие случайной величины.
Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причем заранее неизвестно, какое именно.
Будем обозначать случайные величины заглавными буквами латинского алфавита (Х, Y , Z ,…), а их возможные значения – соответствующими малыми буквами (xi , yi ,…).
Примеры: число очков, выпавших при броске игральной кости; число появлений герба при 10 бросках монеты; число выстрелов до первого попадания в цель; расстояние от центра мишени до пробоины при попадании.
Можно заметить, что множество возможных значений для перечисленных случайных величин имеет разный вид: для первых двух величин оно конечно ( соответственно 6 и 11 значений), для третьей величины множество значений бесконечно и представляет собой множество натуральных чисел, а для четвертой – все точки отрезка, длина которого равна радиусу мишени. Таким образом, для первых трех величин множество значений из отдельных (дискретных), изолированных друг от друга значений, а для четвертой оно представляет собой непрерывную область. По этому показателю случайные величины подразделяются на две группы: дискретные и непрерывные.
Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями.
Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток.