Раздел 3. Теория игр и политология
Лекция 7. Применение теории игр к анализу выборов и голосования в коллективных органах
1. Игры на оптимальное размещение (location games).
2. Приложение к оптимизации предвыборной платформы.
3. Учет политического спектра избирателей.
4. Образование коалиций при участии трех игроков и более. Кооперативные игры.
5. Коалиционные модели с индексами влияния фракций.
1. Приступим к рассмотрению игр, которые имеют, так сказать, практическое приложение. Начнем с игры, которая по самому смыслу исключает возможность применения смешанных стратегий. В таких играх на размещение, с которыми мы сейчас ознакомимся, основная трудность состоит в составлении самой матрицы игры, то есть в вычислении выигрышей игроков при разных комбинациях их чистых стратегий. Классическая формулировка этой игры такова: два продавца прохладительных напитков устанавливают свои палатки на пляже, разделенном на 9 секторов, последовательно пронумерованных. В каждом секторе одинаковое количество потенциальных покупателей, причем каждый из них покупает воду в ближайшей к нему палатке, а если они одинаково близки – то половина людей из этого сектора пляжа покупает в одной, половина – в другой. Спрашивается – в каком секторе продавцу установить палатку, если второй может свою поставить хоть где, даже в одном секторе с ним. Очевидно, что ситуации соответствует парная игра, в которой у каждого игрока по 9 стратегий (номер стратегии соответствует номеру сектора пляжа, где он поставит палатку). Таким образом матрица игры имеет размерность 9х9. Будем выражать выигрыш первого продавца в числе секторов пляжа, откуда отдыхающие придут к нему. Сразу ясно, что если оба продавца ставят палатки в один и тот же сектор пляжа, то независимо от номера сектора они получат одинаковый выигрыш. Поэтому на главной диагонали матрицы стоят одинаковые числа 9/2 = 4,5. Кроме того, такой же выигрыш будет при симметричном расположении продавцов относительно середины пляжа (то есть в 1-м и 9-м секторах, 2-м и 8-м, 3-м и 7-м, 4-м и 6-м). После этих предварительных замечаний приступим к заполнению матрицы. Если первый продавец ставит палатку в первом секторе, а второй – во втором, то к первому придут отдыхающие только с первого сектора, то есть а12 = 1. Если он ставит в первом секторе, а второй «игрок» - в 3-м, то к первому обратятся люди из первого и половины второго сектора, то есть а13 = 1,5. Соответственно а14 = 2, а15 = 2,5, а16 = 3, а17 = 3,5, а18 = 4 и а19 = 4,5. Теперь приступаем к заполнению второй строки матрицы. Если первый продавец ставит палатку во втором секторе, а второй – в первом, то к первому обратится 8 секторов, поэтому а21 = 8. И так далее. В результате получим следующую матрицу выигрышей первого игрока:
1) 4,5 1 1,5 2 2,5 3 3,5 4 4,5 | 1
2) 8 4,5 2 2,5 3 3,5 4 4,5 5 | 2
3) 7,5 7 4,5 3 3,5 4 4,5 5 5,5 | 3
4) 7 6,5 6 4,5 4 4,5 5 5,5 6 | 4
5) 6,5 6 5,5 5 4,5 5 5,5 6 6,5 | 4,5
6) 6 5,5 5 4,5 4 4,5 6 6,5 7 | 4
7) 5,5 5 4,5 4 4,5 3 4,5 7 7,5 | 3
8) 5 4,5 4 3,5 3 2,5 2 4,5 8 | 2
9) 4,5 4 3,5 3 2,5 2 1,5 1 4,5 | 1
Для удобства строки матрицы, соответствующие номерам стратегий (выбранному номеру сектора пляжа), здесь занумерованы, а справа выписаны минимумы для каждой строки. Хорошо видно, что минимаксной стратегией здесь является пятая. Установив палатку в 5-м секторе (то есть посередине пляжа) первый продавец гарантирует себе выигрыш 4,5 независимо от того, где поставит палатку второй продавец. У второго игрока тоже оптимальной является 5-я стратегия. Если один из игроков придерживается такой стратегии, а другой – нет, то последний получает меньше, чем 4,5. Заметим, что эта игра с ненулевой суммой (биматричная) и поэтому необходимо отдельно рассматривать еще и матрицу выигрышей второго продавца. Обычно обе эти матрицы совмещают в виде одной со сдвоенными элементами, но в данном случае это будет слишком громоздко. Номерам стратегий второго игрока как обычно соответствуют номера столбцов, поэтому матрица второго игрока здесь получается из матрицы первого транспонированием, например ее первая строка будет такой же, как первый столбец исходной. У второго игрока тоже оптимальной является 5-я стратегия. Если первый избрал рекомендованную стратегии, а второй – нет, то выигрыш первого может только увеличиться (до 6,5), а выигрыш второго будет всегда меньше, чем 4,5.
Конечно, неприятно выписывать такие большие матрицы. Зато картина сразу становится предельно ясной. К тому же часто выявляются какие-нибудь закономерности, облегчающие работу. Например, здесь достаточно вычислить лишь первые 5 строк – остальные их повторяют в обратном порядке (последняя – первую, предпоследняя – вторую и т.д.). А элементы матрицы второго игрока можно сразу вычислять как разность между 9 и соответствующим элементом первой матрицы. Кстати именно потому, что выигрыши игроков жестко связаны, рассмотренная игра относится к сильно конкурентным играм, которые по сути близки к антагонистическим. Действительно, если в качестве выигрыша рассматривать разницу между обратившимся к продавцу числом секторов и «законной половиной» клиентов (для этого надо просто вычесть 4,5 из элементов обоих матриц), то получим игру с нулевой суммой. При этом набор стратегий (5 и 5) соответствует седловой точке.
2. Понятно, что вы себя готовите не для того, чтобы содовой на пляже торговать. Поэтому рассмотрим задачу из области политологии, которая решается аналогичным образом. Два кандидата борются за голоса избирателей в округе, причем спектр политических предпочтений избирателей очень широк. Его можно разделить на 9 интервалов («левые», «умеренные» и т.д.). Для простоты будем считать, что на каждый такой интервал приходится по 10000 избирателей. Не правда ли это очень похоже на задачу про пляж? Надо только элементы в игровой матрице умножить на 10000 – и подсчитывай голоса в зависимости от выбранной точки на политическом спектре! То есть мы получили инструмент для моделирования исходов выборов в зависимости от заявленной платформы каждого из кандидатов.
В связи с вышеизложенным ясно, что обоим кандидатам стоит придерживаться 5-го интервала спектра при неопределенной позиции противника. Используя матрицу выигрышей нетрудно сказать и какой стратегии лучше придерживаться при заявленной позиции второго кандидата – это просто задача на оптимальный ответ при известной матрице игры. Можно аналогичным образом решать и более сложные задачи. Проведем например анализ шансов на победу в выборах первого кандидата в предположении, что для второго кандидата равновероятен любой интервал политического спектра. Вероятное число голосов, которое получит первый кандидат, придерживающийся i-го интервала спектра, в этом случае равно среднему значению элементов i-ой строки. Имеется в виду, что элементы полученной ранее матрицы выражают собой число голосов, поданных за первого кандидата, в единицах 10 тыс.голосов. Достаточно просто сложить элементы каждой строки и разделить сумму на 9 (число интервалов политического спектра). Полученные значения приведены в таблице.
Таблица 1.
Вероятное число голосов в зависимости от выбранного интервала политического спектра.
| Номер интервала | 7 | 8 | 9 |
| Число голосов, тыс.чел. | 49,4 | 41,1 | 30,6 |
Поскольку полное число голосов равно 90 тысяч, то для победы достаточно 45 тыс. плюс один голос. Таким образом, при сделанных предположениях этому условию удовлетворяют интервалы с 3-го по 7-й.
Рассмотренную модель голосования легко обобщить на случай неравномерного политического спектра избирателей. Например, зададим в 6 и 7 интервалах большее число избирателей, чем в других. Пусть в этих интервалах будет по 15000 избирателей, а в остальных – по прежнему по 10000. В этом случае придется пересчитать матрицу выигрышей, имея в виду, что «статистический вес» выделенных секторов стал теперь 1,5. Про симметрию теперь можно забыть, все элементы придется считать «в лоб» (хотя на главной диагонали по прежнему оба кандидата делят голоса пополам). Рассуждать лучше так, как будто вы на пляже: «Если я займу первый сектор, а он второй, то ко мне придут только из первого сектора» и т.д. Поскольку полное число голосов теперь равно 100 тысяч, то запишем матрицу игры в форме отклонения набранных голосов от «законных» 50 тысяч, что соответствует игре с нулевой суммой. Матрица в этом случае кстати получается кососимметричной, то есть зеркально симметричной относительно главной диагонали с точностью до знака (он разный у симметричных элементов). Игры с матрицей такого типа называются симметричными. В нашем случае элементы матрицы равны числу избыточных или недостающих голосов (в тысячах) по сравнению с половиной всех голосов при разных наборах чистых стратегий кандидатов:
1) 0 -40 -35 -30 -25 -20 -15 -10 -5 | -40
2) 40 0 -30 -25 -20 -15 -10 -5 0 | -30
3) 35 30 0 -20 -15 -10 -5 0 7,5 | -20
4) 30 25 20 0 -10 -5 0 7,5 15 | -10
5) 25 20 15 10 0 0 7,5 15 22,5 | 0*
6) 20 15 10 5 0 0 15 22,5 30 | 0*
7) 15 10 5 0 -7,5 -15 0 30 35 | -7,5
8) 10 15 0 -7,5 -15 -22,5 -30 0 40 |-22,5
9) 5 0 -7,5 -15 -22,5 -30 -35 -40 0 | -22,5
____________________________________________
40 30 20 10 0 0 15 30 40
* *
Классический анализ с нахождением максимального минимума по строкам и минимального максимума по столбцам (они обозначены звездочками) дает, что игра имеет 4 седловые точки, то есть решается в чистых стратегиях. Обоим кандидатам следует придерживаться 5-го или 6-го интервалов спектра. При этом им гарантируется по 50% голосов. Разумеется, подобная теоретико-игровая модель дает прогноз с разумной точностью и от ее нельзя требовать результатов расчетов с погрешностью в один голос из 100000 поданных голосов.
3. Аналогичная игровая модель может использоваться и в том случае, когда предпочтения избирателей (политический спектр) заданы некоторой функцией. При этом достаточно провести аппроксимацию этой непрерывной функции гистограммой, искусственно разбив весь спектр на определенное число интервалов. В каждом из интервалов теперь в принципе может быть любое число голосов избирателей, в том числе, например, разное во всех интервалах. Обычно используется однопиковая функция, определенная на отрезке [0,1] оси Х одномерного политического пространства. Точка xи, на которую приходится максимум этой функции, называется идеальной. Левый склон пика соответствует избирателям левого толка, правый – правого. Например, применяют функцию вида:
f(x) = a + b│x - xи│
Здесь a и b – численные коэффициенты, задающие общее число избирателей и крутизну пика. Рассмотренный выше пример с равномерным спектром соответствует значению b=0. В принципе, идеальная точка может располагаться и на границе области определения, тогда спектр имеет вид обычной линейной функции.
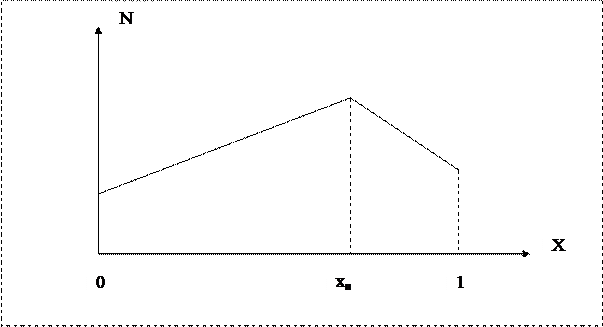
После разбивки отрезка [0,1] на интервалы количество избирателей в каждом из них определяется значением спектральной функции на середине интервала. Поскольку в расчетах используется по существу численная аппроксимация спектральной функции, то она может быть любой, в том числе многопиковой. Можно вообще задать ее сразу просто таблицей, составленной на основе социологических опросов. Тогда те же интервалы, что и в таблице, непосредственно используются в игровой модели.
Далее повторяется процедура с составлением матрицы игры по аналогии с продавцами на пляже, число секторов которого равно теперь заданному числу интервалов. Рекомендуется также записать ее в форме отклонения от половины имеющихся голосов, после чего провести классический анализ для игр с нулевой суммой. Конечно, и у такой модели есть недостатки. Так, не учитывается возможность отказа некоторых избирателей от голосования. Более сложные модели учитывают еще и затраты на предвыборную агитацию. Для этого из элементов уже составленной матрицы игры вычитают некий эквивалент затрат на политическую рекламу среди соответствующей группы избирателей.
4. До сих пор мы рассматривали только парные игры. Однако в политологии часто встречаются ситуации, в которых одновременно участвует более чем 2 взаимодействующих стороны. Это, например, участие нескольких кандидатов в выборах, голосование разных фракций в парламенте, принятие решений в коллективных органах типа НАТО или Европарламента. В этом случае необходимо использовать теоретико-игровые модели с числом игроков 3 и более, которые существенно отличаются от уже изученных нами игр. Основные особенности таких игр хорошо проявляются уже на примере игры всего с тремя участниками. Даже если это игра с нулевой суммой, интересы игроков теперь не обязательно противоположны, как это было в антагонистических играх. Дело в том, что теперь вполне возможна ситуация, когда двум игрокам выгодно объединиться против третьего. То есть когда действуя по одиночке они в сумме выиграют меньше, чем объединив усилия. Можно привести массу примеров, когда это действительно имеет место, достаточно вспомнить хотя бы совместное голосование фракций в парламенте или военные союзы. Выбор стратегии каждого игрока в этом случае сводится к выбору наиболее выгодных для него союзников. Объединение игроков с целью максимизации общего выигрыша в теории игр принято называть коалицией. Функция ν(S), которая описывает зависимость суммарного выигрыша коалиции от ее состава и размера, называется характеристической функцией. В свою очередь игры, допускающие образование коалиций, называют кооперативными играми. Для решения таких игр необходимо рассмотреть все возможные коалиции и оценить их с точки зрения полезности для каждого игрока. После выделения устойчивых коалиций их можно рассматривать как отдельных игроков, что сразу упрощает анализ игры. Например, в парламенте формируется в этом смысле всего 2 коалиции (правящая коалиция и оппозиция), так что по сути игра сводится к парной, решение которой хорошо известно. После этого решается задача дележа выигрыша между членами коалиции с учетом возможных выигрышей этих игроков в составе других коалиций. Число возможных коалиций и сложность решения таких игр быстро возрастают с увеличением числа игроков n и на сегодняшний день более-менее изучены только игры с n<5.
Для примера рассмотрим простую игру трех лиц с нулевой суммой. Пусть правила таковы, что любые 2 игрока, вступившие в коалицию, получают суммарный выигрыш 1. Третий игрок при этом проигрывает 1, то есть его выигрыш равен -1. В данном случае удобно воспользоваться таблицей, аналогичной нормальной форме игры, только теперь строки соответствуют разным коалициям, а столбцы – игрокам.
Таблица 1
Матрица выигрышей игроков в составе разных коалиций
| Игроки Коалиции | 1 | 2 | 3 |
| (1,2) | 1/2 | ½ | -1 |
| (1,3) | 1/2 | -1 | 1/2 |
| (2,3) | -1 | ½ | 1/2 |
Данная игра является симметричной и поэтому характеристическая функция зависит только от размера коалиции m. В табл.2 она задана таблично. В общем случае в первом столбце указывается состав коалиции, т.е. рассматриваются значения характеристической функции ν(1,2), ν(1,3) и т.д.
Таблица 2
Характеристическая функция коалиций
| m | ν |
| 0 1 2 3 | 0 -1 1 0 |
Иногда используют и обычную нормальную форму игры, которая в данном случае имеет вид двух матриц, соответствующих выбору третьим игроком коалиции с 1-м и со 2-м игроками. При этом в ячейках таблицы придется указывать выигрыши каждого из игроков, как это делается для игр с ненулевой суммой. Очевидно, для анализа удобнее форма, представленная в табл.1.
В данном случае возможны 3 коалиции. Все они устойчивы, так как переход в к другой коалиции не повышает выигрыш хотя бы одного участника действующей коалиции. При попытках не вошедшего в коалицию игрока создать другую коалицию, один из коалициантов будет против (его выигрыш уменьшится до -1), а другой – безразличен (его выигрыш останется 1.2). Конечно, его можно попытаться переубедить, предложив дополнительное вознаграждение за счет третьего игрока (при создании новой коалиции его выигрыш возрастет с -1 до ½), но это противоречит правилам данной игры, предусматривающей равномерный дележ внутри коалиции. Разные правила игры соответствуют разным нормам поведения, принятым в обществе. Коалициант может отказаться от перехода в более выгодную для него коалицию по этическим, идейным или религиозным соображениям. Таким образом, в зависимости от существующих норм поведения игра может иметь разное решение при той же матрице игры.
Анализ общей игры трех лиц с неравномернцм дележом приводит к весьма неожиданным выводам. Например, если только один из игроков обладает правом получения более половины выигрыша коалиции в ущерб своего партнера по коалиции, то остальные игроки просто не будут участвовать в коалиции с ним – им выгоднее коалиция с обычным игроком. В этой ситуации привилегированный игрок будет вынужден сам предлагать партнеру компенсацию, чтобы не оказаться в проигрыше. Строгое решение игры с произвольным дележом выигрышв было получено Нейманом графическим методом. Он рассматривал трехмерный вектор выигрышей α = (α1, α2, α3,) на плоскости с тремя осями α1, α2, α3, под углом 60о друг к другу (компоненты вектора – это выигрыши игроков). Из условия ограничения на размер проигрыша (αi≥ -1) можно сделать вывод, что решение находится внутри области, ограниченной «фундаментальным» треугольником (рис.1). Причем устойчивым оказывается дележ вида:
α = (a, b, -a -b) ,
где константы a и b удовлетворяют условию -1 ≤ b ≤ 1-a. Это семейство решений явно не симметрично относительно игроков и означает следующее. Один из игроков (для определенности, третий) сразу исключается из процесса переговоров о создании коалиции. Переговоры ведутся между 1-м и 2-м игроками о разделе между ними суммарного выигрыша и о величине проигрыша 3-го игрока. Решение лишь оговаривает интервал для этого проигрыша и ничего не говорит о пропорции между выигрышами первого и второго игрока. То есть в принципе весь выигрыш может забрать, например, первый игрок – второй все равно не выйдет из коалиции, так как на заключение коалиции с третьим игроком наложен запрет. Именно поэтому коалиция и оказывается устойчивой. Нечто похожее отмечалось в последние годы в работе Верховной Рады Украины, когда представители оранжевой коалиции заявляли о недопустимости переговоров с партией Регионов по идейным соображениям. То есть из трех основных игроков – блока БЮТ, блока Наша Украина-Народная самооборона и партии Регионов последний был исключен по всем правилам теории игр. Заметим, что переход депутатов из одной фракции в другую требует рассмотрения каждого депутата в виде отдельного игрока, что приводит к практически не решаемой задаче с 450 игроками.
5. Может создаться впечатление, что теория игр способна полностью объяснить, например, образование и распад коалиций в парламенте, рассмотрев игру, в которой коалиции образуются отдельными игроками-парламентариями. На самом деле коалиционные игры удается теоретически описать лишь при небольшом числе игроков - уже при n = 4 геометрическая интерпретация игры связана с рассмотрением трехмерного куба как области возможных решений. Поэтому при n ≥ 4 теория коалиционных игр рассматривает лишь некоторые частные случаи, как правило те, когда игра распадается на более простые подъигры (например на игру 3-х лиц и «болвана»(dummy)). А в том же парламенте Украины, например, 450 депутатов, так что говорить о полном теоретическом описании ситуации здесь явно не приходится. На практике образование коалиций в парламенте обычно описывают не как игру всех взаимодействующих депутатов, а как образование коалиций из фракций, число которых не столь велико. Численность фракций при этом учитывается введением статистических весов для макроигроков, участвующих в голосовании.
Рассмотрим голосование в парламенте, состоящем из 3-х фракций: левых (Л), правых (П) и партии центра (Ц). Пусть численность этих фракций составляет соответственно 49, 1 и 50 депутатов. Предположим, что для принятия определенного законопроекта необходимо набрать простое большинство голосов, то есть хотя бы 51 голос. Ясно, что ни одна из фракций столько голосов не имеет, поэтому необходимо создать коалицию, насчитывающую достаточное количество голосов. В принципе, получается та же игра трех лиц, рассмотренная выше, но с некоторыми изменениями. Во первых, будем считать, что в случае создания достаточно влиятельной коалиции ее выигрыш равен 1, тогда как в противном случае он равен 0. Заметим, что это уже игра с ненулевой суммой и, например, выигрыш коалиции из всех 3-х фракций здесь равен 1. Это так называемая простая игра описывается как и прежде характеристической функцией, которая может принимать всего два значения: 0 и 1. Она описывается заданием выигрыша для всех возможных коалиций:
ν(Л,П) = 0
ν(Л,Ц) = 1
ν(П,Ц) = 1
ν(Л,Ц,П) = 1
Формально можно рассматривать коалиции из одной фракции (их 3 и для всех ν = 0) и даже коалицию, состоящую из пустого множества: ν(Φ) = 0. Итого получается 8 возможных коалиций. В игре n лиц число всех таких возможных поднаборов игроков равно 2n, что при n=3 как раз и равно 8. Из них выигрышными являются в данном случае только 3.
Принято оценивать роль отдельных фракций по числу выигрышных коалиций, в которую они входят. Причем особое значение имеют такие коалиции, которые перестают быть выигрышными при выходе из нее данной фракции. Например, игрок П входит в 2 выигрышные коалиции, но только в одной из них (Ц,П) он является критически важным. Аналогично и игрок Л может разрушить своим выходом только одну из выигрышных коалиций (Л,П). В то же время игрок Ц критически важен для всех трех выигрышных коалиций. Отношение числа выигрышных коалиций, для которых участие данной фракции является критичным, к полному числу таких минимально выигрышных коалиций, называется индексом Банцафа фракции. Таким образом, индекс Банцафа описывает роль отдельных фракций не столько в образовании коалиций, сколько в их распаде. Коалиция из двух партий может распасться при выходе либо первой фракции, либо второй. Поэтому при расчете знаменателя индекса Банцафа каждая такая коалиция учитывается дважды, то есть коалиции (Ц,П) и (Л,Ц) вместе дают 4 минимально выигрышных коалиций. Коалиция из трех партий может стать невыигрышной только при выходе из нее фракции Ц, поэтому она учитывается 1 раз. В результате получаем 5 минимально выигрышных коалиций, и индекс Банцафа для фракций Л,Ц и П равен 1/5, 3/5 и 1/5 соответственно.
Влияние разных фракций в коалиции описывается также индексом Шепли-Шубика. Этот индекс описывает как раз процесс создания выигрышной коалиции. Причем опять учитывается, какая именно фракция присоединяется к другой, то есть инициирует контакт. В нашем примере каждая из 3-х фракций может присоединиться к одной из двух других и в этом смысле существует всего 6 сценариев образования коалиции из двух фракций. Если предположить, что все они равновероятны, то вероятность каждого из них равна 1/6. Образование коалиции из трех игроков происходит при присоединении к уже образованной коалиции из двух фракций единственной оставшейся. Индекс Шепли-Шубика учитывает число сценариев, при которых присоединение данной фракции к коалиции приводит к созданию выигрышной коалиции (до ее присоединения голосов не хватало). Точнее говоря этот индекс равен среднему по всем сценариям выигрышу, который дает присоединение данной коалиции. Рассмотрим например фракцию П. Ее присоединение дает выигрыш 1 только в одном случае - когда П присоединяется к Ц. В остальных 5 сценариях она не приносит выигрыш и поэтому для нее индекс Шепли-Шубика равен:
1*1/6 + 0*1/6 + 0*1/6 + 0*1/6 +0*1/6 + 0*1/6 = 1/6
Точно также показывается, что для фракции Л этот индекс тоже равен 1/6, а для фракции Ц 4/6 = 2/3. Заметим, что эти значения отличаются от полученных ранее оценок индекса Банцафа, хотя в обоих случаях у фракции Ц индекс заметно больше, чем у других фракций.
На примере голосования 4-х фракций можно пояснить понятие «болвана» в коалиционных играх. Пусть у первой фракции 1 голос, у второй – 2, у третьей – 3 и у четвертой – 4. Всего получается 11 голосов, так что выигрышной является коалиция, насчитывающая хотя бы 6 голосов. Ясно, что в любой выигрышной коалиции можно обойтись без 1-го игрока, то есть он никогда не является критичным или приносящим выигрыш. Такие игроки и называются «болванами». Значение обоих рассмотренных индексов для 1-й фракции равно 0, для трех других оба индекса равны 1/3.
Вопросы:
1. Построение платежной матрицы в играх на размещение (location games) на примере выбора места торговли на пляже двумя торговцами водой.
2. Выявление минимаксных и доминируемых стратегий игроков.
3. Определение наилучшей ответной стратегии (BR).
4. Применение игры к определению оптимальной предвыборной стратегии на выборах с 2 кандидатами и равномерным спектром избирателей.
5. Определение стратегии, обеспечивающей наибольшую вероятность победы на выборах, и стратегии, гарантирующей определенное количество голосов.
6. Построение игровой матрицы при неравномерном спектре избирателей.
7. Игровая модель при 3 кандидатах на выборах.
8. Представление и анализ матрицы игры в случае дискретного политического спектра избирателей
9. Как подсчитывается суммарный выигрыш коалиции?
10. Оценка роли коалиции в парламенте.
11. Что обозначает и как подсчитывается индекс Банцаафа?
12. Что характеризует индекс Шепли-Шубика?
13. Поясните понятие «болвана» в коалиционных играх.
Литература:
Учебные пособия и монографии:
1. Алескеров Ф., Ортешук П. Выборы. Голосование. Партии. - М.: Академия, 1995. – 84 с.
2. Алескеров Ф.Т. и др. Влияние и структурная устройчивость в Российском парламенте (1905-1917 и 1993-2005 гг.). – М.: ФИЗМАТЛИТ, 2007. – 312 с.
3. Клима Р.Э., Ходж Дж.К. Математика выборов: Пер. с англ. – М.: МЦНМО, 2007. – 224 с.
4. Мулен Э. Теория игр с примерами из математической экономики: Пер. с франц. – М.: Мир, 1985. – 200 с.
5. Binmore K. Game Theory. A very short introduction. Oxford University Press, 2007.
6. Brams Steven J. Game Theory and Politics. Dover Publications, 2004.
7. Gates S., Humes B. Games, Information and Politics. Applying Game Theoretic Models to Political Science. The University of Michigan Press, 2007.
8. Mayerson R.B. Game Theory. Analysis of Conflict. Harvard University Press, 1997.
9. Ordeshook Peter C. Game Theory and Political Theory. Cambridge University Press, 2003.
10. Watson J. Strategy. An Introduction to Game Theory. W.W.Norton & Company, 2002.








