Рис. 0. Представление динамики переговоров игрой в развернутой форме.
В классической теории игр обычно предполагается, что игроки выбирают свою стратегию одновременно и независимо друг от друга. На примере ультимативных игр мы видим, что в ряде случаев игроки делают свой выбор в разные моменты времени, причем результат игры зависит от последовательности, в которой игроки принимают решение. Причем второй игрок при этом делает выбор, уже зная выбор первого игрока. С другой стороны, бывают случаи, когда игроки принимают решение совместно, а не по одиночке – так происходит при подписании договоров, контрактов, вступающих в силу лишь после того, как все стороны поставили свои подписи. В последние годы развита целая техника отображения таких специфических моментов переговоров игрой в развернутой форме. Как и в обычной экстенсивной форме игры ситуация отображается в виде графа. Точки принятия решения отдельными игроками изображаются на нем обычными черными точками с указанием номера игрока рядом с ней. Выбор определенной стратегии отображается стрелкой. Точкам принятия совместных решений сразу несколькими игроками соответствуют точки, обведенные кружком. Если стратегией игрока является выбор определенного значения из заданного интервала чисел (например, цены на газ для Украины), то это отображается сектором дугой между двумя отрезками, выходящими из точки принятия решения. Выбору стратегии при этом соответствует точка дуги, из которой выходит стрелки, описывающие стратегии другого игрока (рис.1).
Над сектором указывают обозначение параметра, выбор значения которого осуществляется первым игроком. Возле стрелок, соответствующих концу игры, указываются через запятую выигрыши каждого игрока. Именно так изображаются, например, те же ультимативные игры.
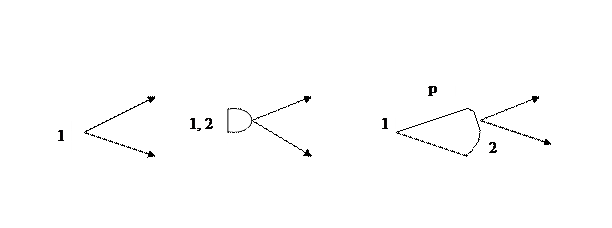
Рис.1. Характерные элементы графа, отображающего ведение переговоров.
Различные комбинации таких элементов образуют достаточно сложный граф, отображающий ход переговоров. Такое представление удобно для количественного анализа последствий отдельных решений, сделанных в ходе переговоров.
Выбрав наиболее выгодный конечный вариант по величине выигрыша, приведенной в конце графа, можно методом обратной индукции определить всю последовательность оптимальных решений в ходе переговоров.
Вопросы:
1. Какой параметр максимизируется в ходе переговоров о совместном проекте двух сторон?
2. Как определяются компенсационные выплаты в простой договорной игре?
3. Построить игровую модель переговоров о продажет ненужной вещи, представляющей ценность для покупателя..
4. Модель ультимативной игры как пример динамической игры.
5. Примеры игр с точками совместных решений.
6. Описать ход переговоров по данной схеме в виде развернутой формы игры (рис.2).
Литература:
Учебные пособия и монографии:
1. Лефевр В.А., Смолян Г.Л. Алгебра конфликта. Изд. 2-е, стереотипное. – М.: КомКнига, 2007. – 72 с.
2. Оуэн Г. Теория игр: Пер. с англ. – М.: Мир, 1971. – 229 с.
3. Петросян Л.А., Зенкевич Н.А., Семина Е.А. – М.: Высш. шк., Книжный дом «Университет», 1998. – 304 с.
4. Шеллинг Т. Стратегия конфликта: Пер. с англ. – М.: ИРИСЭН, 2007. – 366 с.
5. Axelrod R. The Evolution of Cooperation. Basic Books, 2006.
6. Brams Steven J. Game Theory and Politics. Dover Publications, 2004.
7. Brodie B. Strategy in the Missile Age. Princeton University Press, 1959
8. Diplomacy Games. Formal Models and International Negotiations. Edited by Rudolf Avenhaus & I.William Zartman. Springer 2007.
9. Gates S., Humes B. Games, Information and Politics. Applying Game Theoretic Models to Political Science. The University of Michigan Press, 2007.
10. Mayerson R.B. Game Theory. Analysis of Conflict. Harvard University Press, 1997.
Статьи в периодических изданиях:
11. Kennedy P., Von Witzke H., Roe T. Multilateral agricultural trade negotiations: a non-cooperative and cooperative game approach. European Review of Agricultural Economics Vol. 23 (1996), pp. 381-399.
12. Morrow James D. Capabilities, Uncertainty, and Resolve: A Limited Information Model of Crisis Bargaining. American Journal of Political Science, Vol. 33, No. 4 (Nov., 1989), pp. 941-972.
13. Saaty Th.L. The U.S.-OPEC Energy Conflict. The Payoff Matrix by the Analytic Hierarchy Process. International Journal of Game Theory, Vol. 8, Issue 4, 1979, pp. 225-234.








