4. Brams Steven J. Game Theory and Politics. Dover Publications, 2004.
5. Brodie B. Strategy in the Missile Age. Princeton University Press, 1959
6. Diplomacy Games. Formal Models and International Negotiations. Edited by Rudolf Avenhaus & I.William Zartman. Springer 2007.
7. Gates S., Humes B. Games, Information and Politics. Applying Game Theoretic Models to Political Science. The University of Michigan Press, 2007.
8. Kahn H., Mann I. Game Theory. Rand Corporation, 1957.
9. Mayerson R.B. Game Theory. Analysis of Conflict. Harvard University Press, 1997.
10. Rapoport A. Two-person Game Theory. Dover Publications, 1999.
Статьи в периодических изданиях:
11. Brams Steven J., Kilgour D.M. National Security Games. Synthese 76 (1988), pp. 185-200.
12. Kraig Michael R. Nuclear Deterrence in the Developing World: A Game-Theoretic Treatment. Journal of Peace Research, Vol 36, No.2, 1999, pp. 141–167.
13. Myerson Roger B. Game-Theoretic Consistency and International Relations. Journal of Theoretical Politics Vol. 18, No. 4, 2006, pp.416–433.
14. Schwarz M., Sonin K. A Theory of Brinkmanship, Conflicts, and Commitments. The Journal of Law, Economics, & Organization, Vol. 24, No. 1, 2007.
Лекция 5. Игры с неполной информацией и дезинформацией
1. Виды неопределенностей. Роль точности оценки выигрышей
2. Игры с сигнализацией и дезинформацией.
3. Экстенсивные формы представления игры с учетом неопределенности.
1. Для многих конфликтных ситуаций характерна неопределенность их исхода. Собственно, именно поэтому каждый участник конфликта и вступает в борьбу, надеясь на благополучный для себя исход. То есть существует некоторая вероятность каждого возможного исхода. В теории игр выделяют 3 основных типа неопределенностей, которые и дают название соответствующим играм. К первому относится статистическая неопределенность, связанная с использованием в игре датчиков случайных чисел. Это может быть бросание игральных костей, раздача карт или вращение рулетки. В принципе можно рассчитать вероятность различных исходов при этом (обычно используется равномерное распределение вероятности) и, соответственно, рассчитать средний выигрыш. Игры с данным типом неопределенности называются азартными, что видимо связано со словом hazard (франц.) - случай. Для таких игр важнее соображения из области психологии, чем математическая теория.
Второй тип неопределенностей связан с так называемыми комбинаторными играми. Это игры типа шахмат, в которых игрок стоит перед выбором из огромного числа вариантов ходов, которые он не в силах все «просчитать» в уме и поэтому в какой то мере случайно выбирает очередной ход. То есть оптимальный ход для каждой позиции существует, но его может определить только суперкомпьютер. По мере совершенствования компьютеров и их использования в таких играх шахматы, например, перестанут быть игрой в полном смысле этого слова, результат партии будет предрешен для любой исходной позиции.
Для нас наиболее интересен третий тип неопределенности – стратегическая неопределенность. Она связана с неопределенностью хода противника даже при небольшом числе возможных вариантов. Такую неопределенность создает сам выбор той или иной стратегии противником. Соответствующие игры называют стратегическими. Именно применительно к этим играм и создавалась математическая теория игр. Стратегическая неопределенность является наиболее сложной, что видно на примере известной логической задачи про то, как спросить дорогу, ведущую к деревне лжецов. Если на развилке дороги спросить у местного жителя (неизвестно, лжец он или честный) : «Если бы вы жили в другой деревне, как бы вы ответили на вопрос, ведет ли левая дорога в деревню честных людей?», то, как видно из лингвистической матрицы игры, можно все-таки получить истинную информацию:
Истинный ответ на вопрос
«да» «нет»
Ответ честного нет да
Ответ лжеца нет да
Но это срабатывает только в том случае, если лжец всегда обманывает. Используют даже термин «стратегический лжец» для обозначения человека, который обманывает только тогда, когда это ему выгодно, создавая стратегическую неопределенность.
Неопределенность в игре может быть также связана с неточной информацией о значениях элементов матрицы игры, то есть с их погрешностью. Иногда информация о выигрыше при разных стратегиях настолько скудная, что вместо чисел для элементов матрицы используют лингвистические переменные со значениями типа «мало», «много», «очень много». Дело в том, что если точность, с которой известны элементы матрицы игры, достаточна, для определения максимума или минимума в строках и столбцах матрицы, а значит и седловой точки (если она есть), то уже можно определить оптимальный набор стратегий. И для вычисления цены игры надо достаточно точно знать только элемент матрицы в седловой точке. В каждом случае имея числовую матрицу игры и зная возможную погрешность ее элементов можно проверить устойчивость решения к вариациям элементов матрицы в пределах погрешностей. Такие вариации обычно задают случайным образом с помощью датчика случайных чисел.
2. В классической теории игр обычно рассматриваются игры с полной информацией, когда оба игрока знают все предыдущие ходы и матрицу игры. Кроме того, они знают правила игры, в частности насколько она является соревновательной или даже антогонистической (игра с постоянной суммой). Это позволяет судить о намерениях и возможностях противника и выбирать в соответствии с ними оптимальную стратегию ведения игры. Очевидно, что на самом деле это не всегда так, в том числе в международных отношениях. Информация, касающаяся национальной безопасности, во всех государствах является секретной и даже число стран, обладающих ядерным оружием, точно неизвестно. То есть надо рассматривать игры и с неполной информацией.
Пусть игрок А обладает некой информацией, неизвестной игроку В. Тогда в связи с этим у него 3 возможные стратегии:
- скрыть информацию,
- передать игроку В всю информацию или ее часть,
- дать противнику неверную информацию.
В последнем случае речь идет о дезинформации, вводящей противника в заблуждение относительно ваших намерений. Скажем, перед нападением фашисткой Германии на Советский Союз был заключен пакт о ненападении. В карточных играх такого рода поведение называют блефом. В своей монографии Нейман на 32 страницах рассматривает роль блефа в такой простой карточной игре как покер с одной раздачей по 5 карт каждому игроку и последующим назначением ставок. В частности он отмечает, что без блефа в принципе нельзя выиграть большую сумму даже при очень хорошем раскладе карт. Дело в том, что для достижения такого выигрыша необходимо многократное повышение ставок и если противник будет знать, что вы никогда не блефуете он уже после первых повышений поймет, что у вас хорошие карты и не станет дальше повышать свои. С другой стороны, если вы все время блефуете с плохими картами, противник потребует уже в начале игры раскрыть карты. Таким образом, в принципе необходимо чередовать блеф с честной игрой для получения большого выигрыша.
В играх с нулевой суммой (и стратегически эквивалентных им играх с постоянной суммой) обычно выгодно скрыть информацию об очередном ходе, чтобы противник не мог ответить стратегией оптимального ответа. При смешанных стратегиях для этого используют рандомизацию, то есть выбор очередной чистой стратегии с помощью датчика случайных чисел. На практике чаще просто скрывают информацию. Скажем, невыгодно, чтобы противник знал о готовящемся наступлении. В то же время в других случаях выгоднее дать знать противнику о своих возможностях, чтобы избежать его нападения. Например, Израиль сознательно допустил утечку информации об обладании им ядерной бомбой, чтобы воздействовать на экстремистские круги в арабских странах. Заметим, что все детали атомного проекта при этом не афишировались, чтобы избежать санкций со стороны других государств. Такое дозированное распространение выгодной для данного игрока информации называется сигнализацией. Демонстрация новой военной техники на парадах – это тоже сигнализация.
У менее информированного игрока В при получении информации от игрока А тоже есть 3 стратегии:
- поверить этой информации,
- не верить и пытаться отделить правду от лжи,
- игнорировать полученную информацию.
Причем принято больше доверять информации, проявляющейся в действиях игрока А, чем его словам. Хотя игрок А зная это может имитировать соответствующие действия с целью обмана. Тогда игроку В необходимо предпринять действия, заставляющие игрока А обнаружить его истинные намерения и возможности. Такую стратегию называют скринингом и можно привести много примеров из самых разных областей. У военных это разведка боем, у партизан «проверки на дорогах» подозрительного новобранца, наконец «если друг оказался вдруг и не друг и не враг, а так», то Высоцкий рекомендовал альпинизм («парня в горы тяни, рискни»). Выделяют также стратегию типа побудительной схемы (incentive scheme), при которой противника заставляют проявить своими действиями истинную информацию с помощью штрафов или поощрений. Примером является библейская притча про царя Соломона, рассудившего, кому из двух женщин принадлежит ребенок. Он приказал разрезать ребенка пополам, то есть штрафом для настоящей матери была бы смерть ребенка и она отказалась от претензий на него, чем и подтвердила свои материнские права. На практике конечно применяют более цивилизованные схемы, позволяющие выяснить ценность объекта для игрока. Например, выплачивают большую премию по результатам работы, что заставляет работника полностью проявить его способности. В международных отношениях примером являются инспекции на ядерных объектах Ирана – если бы он обладал атомной бомбой, ему пришлось бы отказать в проведении таких проверок и тогда к нему применили бы экономические санкции.
3. Если в игре присутствует статистическая неопределенность, например значение одного из элементов матрицы игры известно как вероятностная величина, то в развернутой форме игры этому соответствует введение дополнительной точки принятия решения. В отличие от точки, где выбор стратегии делает реальный игрок, эту точку называют точкой случая или точкой выбора природы. Соответствующий кружок не штрихуется и возле него не ставится номер игрока. Стрелками, выходящими из него, изображают возможные «случайные стратегии», причем рядом с ними указывают значение случайного параметра и вероятность его реализации. Рассмотрим в качестве примера парную игру с ненулевой суммой, которая в нормальной форме задана матрицей:
1\2 C D
A x, 9 3, 6
B 6, 0 6, 9
Здесь у каждого игрока по 2 стратегии: у первого А и В, у второго С и D, причем выигрыш первого игрока при комбинации стратегий АС задан случайным числом х. Пусть про него известно, что с вероятностью 1/3 оно равно 0 и с вероятностью 2/3 оно равно 10. Допустим, что первый игрок при выборе своей стратегии знает, какое значение х на самом деле имеет место, тогда как второй не знает этого. Тогда игра в развернутом виде представляется графом, приведенном на рис.1. Пунктир соответствует отсутствию информации о первом игроке у второго игрока.
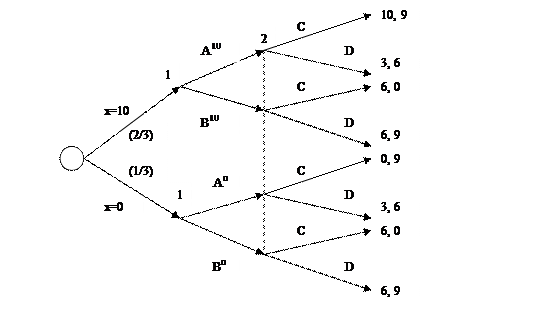
Рис.1. Развернутая форма игры с точкой случая (выбора природы).
Данная игра является асимметричной по информации, так как первый игрок обладает информацией о величине х до выбора своей стратегии, а второй – не знает. Заметим, что при этом у первого игрока теперь как бы 4 стратегии (в том смысле, что стратегия – это инструкция как действовать в зависимости от обстоятельств, например от значения х):
- выбирать при х = 0 стратегию А, и при х = 10 – стратегию А (стратегия А10А0);
- выбирать при х = 0 стратегию А, а при х = 10 – стратегию В (стратегия В10А0);
- выбирать при х = 0 стратегию В, а при х = 10 – стратегию А (стратегия А10В0);
- выбирать при х = 0 стратегию В, и при х = 10 – стратегию В (стратегия В10В0);
Поэтому в обычной нормальной форме игра принимает вид матрицы размерности 4х2. Такая матрица называется нормальной формой по Байесу, потому что значения ее элементов рассчитываются по правилу Байеса для вычисления среднего значения вероятностных величин. Например, элемент, соответствующий набору стратегий В10А0 и D вычисляется с учетом вероятностей реализации разных значений параметра х следующим образом:
(2/3)*(6, 9) + (1/3)*(3, 6) = (5, 8)
Здесь в скобках через запятую указаны компоненты вектора выигрышей игроков. Так, вектор с компонентами (6, 9) соответствует элементу первоначальной матрицы при наборе стратегий В и D, а вектор (3, 6) соответствует стратегиям А и D. В результате таких расчетов получается уже обычная числовая матрица игры, с использованием которой удобно анализировать предпочтительность разных комплексных стратегий. Можно, в частности, найти равновесные по Нэшу наборы стратегий. Так, профиль В10В0 – D здесь является равновесным.
1\2 C D
А10А0 20/3, 9 3, 6
В10А0 4, 3 5, 8
А10В0 26/3, б 4, 7
В10В0 6, 0 6, 9
Некоторые элементы полученной матрицы, например, нижняя строка, полностью совпадают с элементами исходной матрицы. Но вместо случайной величины х теперь в матрицу входят математические ожидания выигрыша с учетом вероятности различных значений х.
Аналогичный подход используется для построения дерева решений в случае, когда решения принимает только одна сторона и известны вероятности их последствий. Это позволяет, в частности, учесть риски при реализации разных стратегий. Пусть, например, у лица, принимающего решение (ЛПР) есть два варианта действий. В первом случае он может получить 10 тыс. у.е. с вероятностью 50%, а во втором – 20 тыс. с вероятностью 10%. Чтобы сделать правильный выбор надо найти математические ожидания выигрыша в обоих случаях и сравнить их. Это «ожидание» рассчитывается как произведение вероятности на величину выигрыша. Таким образом первому варианту соответствует 0,5*10000 = 5000, а второму 0,1*20000 = 2000. Отсюда ясно, что лучше первый вариант.
Вопросы:
1. Какие виды неопределенностей рассматриваются в теории игр?
2. Пояснить решение логической задачи со 100-процентным лжецом.
3. Привести примеры сигнализации из области международных отношений.
4. Привести примеры дезинформации в международных отношениях.
5. Привести примеры скрининга и побудительных схем.
6. Построить нормальную форму игры по Байесу по заданной развернутой форме.
7. Привести пример парной игры с нулевой суммой, в которой оба игрока не знают один из элементов матрицы игры. Как зависят их стратегии от этого элемента?
8. Какая игра называется ассиметричной по информации?
9. Пояснить понятие точки случая (выбора природы). Как она изображается?
Литература:
Учебные пособия и монографии:
1. Лефевр В.А., Смолян Г.Л. Алгебра конфликта. Изд. 2-е, стереотипное. – М.: КомКнига, 2007. – 72 с.
2. Шеллинг Т. Стратегия конфликта: Пер. с англ. – М.: ИРИСЭН, 2007. – 366 с.
3. Axelrod R. The Evolution of Cooperation. Basic Books, 2006.
4. Brams Steven J. Game Theory and Politics. Dover Publications, 2004.
5. Brodie B. Strategy in the Missile Age. Princeton University Press, 1959
6. Davis Morton D. Game Theory: a Nontechnical Introduction. – Dover Publications, 1997.
7. Diplomacy Games. Formal Models and International Negotiations. Edited by Rudolf Avenhaus & I.William Zartman. Springer 2007.
8. Gates S., Humes B. Games, Information and Politics. Applying Game Theoretic Models to Political Science. The University of Michigan Press, 2007.
9. McKinsey J.C.C. Introduction to the Theory of Games. Rand Corporation, 1952.
10. Mayerson R.B. Game Theory. Analysis of Conflict. Harvard University Press, 1997.
Статьи в периодических изданиях:
11. Walsh James I. Do States Play Signaling Games. Cooperation and Conflict: Journal of the Nordic International Studies Association, Vol. 42, No.4, 2007, pp. 441–459.
12. Van Damme E. On the Contributions of John C. Harsanyi, John E Nash and Reinhard Selten. International Journal of Game Theory, Vol. 24, 1995, pp. 3-11.
Лекция 6. Динамические модели переговоров
1. Проблемы переговоров и их игровая интерпретация
2. Стандартное решение «договорной» игры (bargaining)
3. Ультимативные игры
4. Представление динамики переговоров игрой в развернутой форме
1. До сих пор мы рассматривали статические игры, которые являются в принципе одноходовыми, что и позволяет их представить в нормальной форме. Предельным случаем здесь является игра, когда у каждого игрока по одной стратегии, которая состоит в том, чтобы ничего не делать. В этом смысле с помощью таких игр можно анализировать возможные результаты переговоров, а не их процесс. Скажем, при отсутствии договоренностей стороны имели доход d1 и d2, а в случае заключения договора их доход станет v1 v2, причем di < vi. Разница vi – di определяет величину уступки, которая более заинтересованная сторона может предложить менее заинтересованной для подписания договора. Это напоминает ситуацию с заключением контракта, когда в случае отказа от сотрудничества, то есть расторжения договора, сторона-инициатор расторжения выплачивает другой стороне определенную договором компенсацию α. При отсутствии договора стороны тоже могут сотрудничать, если это им выгодно, но контракт повышает устойчивость такого сотрудничества. С точки зрения классической теории игр это парная игра 2х2, стратегиями игроков является участие в договоре или отказ от него. Пусть первая стратегия – участие в сотрудничестве, вторая – разрыв договорных отношений. При отсутствии контракта матрица игры имеет простую структуру:
v1,v2 d1,d2
d1,d2 d1,d2
Введением обязательных компенсационных платежей α и β контракт изменяет как минимум 2 элемента этой матрицы и она принимает вид:
v1,v2 d1+α, d2–α
d1– β, d2+ β d1,d2
Тем самым появляется возможность подкорректировать ее и добиться существования устойчивости по Нэшу в точке а11 (или повышения этой устойчивости). Именно поэтому, кстати желательно присутствие в договоре нескольких корректирующих параметров (α и β в нашем случае), чтобы иметь возможность оптимизировать ситуацию по строкам и столбцам для каждого игрока. Нередко используют, например, третий параметр, описывающий компенсационные выплаты при выходе сразу обеих сторон из договора.
При ведении переговоров в принципе тоже решаются схожие проблемы взаимных уступок. Используя те же обозначения можно сказать, что при заключении договора создается новая ценность, стоимость которой равна:
ΔV = v1+v2 - d1-d2 .
Эту сумму необходимо разделить между высокими договаривающимися сторонами в определенной пропорции, что собственно и должно служить основным предметом переговоров. Если вновь созданная ценность в связи со спецификой вопроса окажется большей частью в распоряжении первой стороны, то логично говорить о некоторой компенсации t, которая первая сторона должна предложить второй. Тогда после подписания договора первая сторона будет иметь v1- t, а вторая v2+ t. При этом очевидно помимо условий равновесия Нэша должны выполняться условия v1- t > d1 и v2+ t > d2 , определяющие так называемую точку несогласия. В этой точке в результате заключения соглашения одна из сторон не получает какого либо преимущества по сравнению с ситуацией, имевшей место до начала переговоров. Соответственно, у ней нет стимула к достижению такого соглашения.
2. Стандартное решение обычной игры такого типа состоит в следующем. Сначала определяются доходы сторон, которые они будут иметь после заключения договора в зависимости от тех или иных условий. Желательно сформулировать эту зависимость от условий путем задания функций v1(х) и v2 (х), где х – переменная, описывающая ситуацию. Например х – это объемы поставок или таможенный тариф. Далее определяется область возможных изменений величины х и находится такое ее значение, при котором суммарный доход договаривающихся сторон будет максимальный. При этом конечно возможны ситуации, при которых это значение х вовсе не максимизирует доходы каждой из сторон в отдельности. После фиксирования оптимального значения х оценивается новая ценность ΔV, которая создается при заключении договора для этого значения х. Естественно, при этом учитываются доходы (или убытки) сторон d1 и d2 на момент подписания договора. Остается определить, как разделить ΔV между партнерами. Обозначим долю первого партнера π1, долю второго π2. Ясно, что π1 + π2 = 1 и оба эти параметра принадлежат интервалу [0, 1]. С учетом значений πi выигрыши сторон после заключения договора составят:
U1 = d1 + π1ΔV
U2 = d2 + π2ΔV .
Соответственно матрица «договорной» игры принимает вид:
U1, U2 d1+α, d2–α
d1– β, d2+ β d1,d2 ,
где α и β – компенсационные выплаты в случае расторжения договора в одностороннем порядке (объявление дефолта). Значения параметров π1, π2, α и β определяются в комплексе не только с учетом политического «веса» сторон, но и из соображений достижения устойчивости по Нэшу в точке а11. В связи с этим U1 должно быть существенно больше d1– β и U2 – существенно больше d2–α. Напомним, что для заключения договора необходимо выполнение еще более сильных неравенств: U1 > d1 и U2 > d2, определяющих точки несогласия. И только после достижения договоренности по долям π1 и π2 определяются компенсации t, которые одна сторона обязуется выплачивать другой в случае заключения договора. Эта сумма по модулю равна просто модулю разности U1 - v1, то есть она полностью определяется оптимальным значением параметра х и согласованным значением доли π1. Причем в тексте договора будет стоять именно значение величины t наряду с параметром х и чтобы понять потом, на каких долях π1и π2, сошлись договаривающиеся стороны придется делать обратный пересчет.
3. До сих пор мы рассматривали игры, в которых сам процесс переговоров фактически не моделируется. Не имело значение, например, кто из игроков делает первый ход, то есть кто вносит предложение о параметрах договора. Стандартное решение такой игры просто не зависит от последовательности поступления предложений от партнеров, в любом случае предложения принимаются или отклоняются только исходя из обсуждаемых значений таких параметров, как d, d2, α и β. В динамических же моделях переговоров рассматривается именно сам процесс «игры», последовательность действий партнеров во времени.
Простейшей такой моделью являются ультимативные игры. Рассмотрим в качестве примера переговоры, происходящие между покупателем и продавцом дома. Пусть ценность дома для покупателя составляет 100 тыс.долларов, а для продавца 50 тыс. Такая разница между оценками стоимости объекта разными договаривающимися сторонами встречается достаточно часто, в том числе в связи с предметами культурной и исторической ценности. Допустим, что переговоры состоят в том, что одна из сторон называет цену, а вторая либо соглашается с ней, либо отказывается от покупки-продажи. В рассматриваемой нами ситуации каждая сторона согласна на цену в интервале от 50 до 100 тыс.долларов. Поэтому все зависит от того, какую конкретно цену в этом интервале предложит первая договаривающаяся сторона. Стратегиями игроков здесь является с одной стороны предлагаемая цена, а с другой – согласие или отказ (см. рисунок). Если это будет продавец, то он назовет 100 тыс. (при условии, если ему известна оценка дома покупателем) и покупатель согласится, ведь он при этом ничего не теряет. То есть это будет равновесная по Нэшу цена, устраивающая обе стороны. Если же первым цену называет покупатель, то он назовет 50 тыс. и это тоже будет равновесие по Нэшу, потому что эта цена максимально устраивает обе стороны в новых условиях. Таким образом, результат переговоров в данном случае зависит не только от оценки стоимости объекта сторонами, то есть от значения элементов матрицы выигрышей, но и от самой процедуры переговоров, от их регламента.