Раздел 2. Теоретико-игровой анализ международных отношений
Лекция 4. Простые игровые модели международных конфликтов
1. Теоретико-игровой анализ Карибского кризиса.
2. Применение вероятной (дозированной) угрозы (brinkmanship).
1. Рассмотрим применение теории игр к анализу международных отношений на примере Карибского кризиса. В сентябре-октябре 1962 г. Советский Союз развертывал на западе Кубы ракетную базу. Уже было установлено около 40 ракет с ядерными боеголовками, дальность действия которых позволяла поразить большинство городов и военных объектов США. Ракеты доставлялись на Кубу морем в обстановке полной секретности - даже капитаны судов не знали, что за груз у них на борту. База должна была быть полностью оборудована к середине ноября, но 14 октября самолет-разведчик США сфотографировал уже развернутые ракеты и 16 октября после расшифровки снимков информацию о развернутых ракетах и средствах их защиты сообщили президенту США Дж.Кеннеди. Тот сразу провел совещание в узком кругу экспертов и в течение недели принял решение объявить морскую блокаду Кубы. США требовали убрать ракеты, угрожая драматическими последствиями. Советский лидер Никита Хрущев тоже выступил с воинственными заявлениями. В результате 2 недели мир стоял на грани ядерной войны. 26 октября Кеннеди объявил ультиматум, требуя в 24 часа принять решение о демонтаже ракет в обмен на обещание США отказаться от нападения на Кубу. Руководство США объявило мобилизацию резервистов и стало готовиться к нанесению удара по базе (а возможно и по СССР). Было принято решение о начале военных действий при игнорировании ультиматума не позднее 29 октября. Но 27 октября Хрущев согласился убрать ракеты с Кубы и конфликт был исчерпан. К 20 ноября ракеты были вывезены с Кубы.
Эти события можно представить в виде парной игры следующим образом. Первый игрок (США) после развертывания советских ракет у своих границ выбирает одну из двух возможных стратегий – либо угрожать СССР военными действиями вплоть до полномасштабной ядерной войны, либо смириться с новой угрозой для США. В последнем случае игра заканчивается. В случае объявлении угрозы второй игрок (СССР) в свою очередь стоял перед выбором – демонтировать ракеты, чтобы избежать ядерного конфликта, или защищать свою первую военную базу вне территории СССР всеми средствами (которых было вполне достаточно). После этого выбора игра заканчивается и определяются выигрыши игроков. Это игра с ненулевой суммой, которая в экстенсивной форме имеет вид, показанный на рис.2. Само дерево игры здесь не вызывает сомнений, проблема только с определением выигрышей игроков.
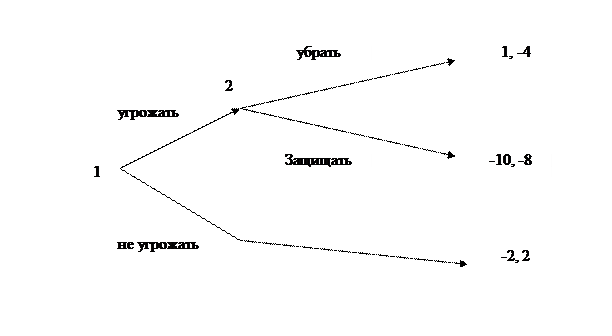
Рис. 2. Простая модель Кубинского кризиса.
В случае отказа США от противодействия развертыванию базы, точнее говоря, от угрозы ответных действий, СССР получал военное и политическое преимущество, которые соответственно теряли США. Поэтому выигрыши игроков условно можно оценить как (-2, 2). В случае принятия решений о военном противостоянии с обоих сторон произошел бы ядерный конфликт с большими человеческими жертвами. То есть в этом смысле проиграли бы оба игрока и очень сильно. Все же у США проигрыш был бы больше, поскольку там выше стоимость жизни, а население СССР выше ставило государственные интересы и в каком то смысле спокойней относилось к войне после сравнительно недавней войны с фашистской Германией. Поэтому при таком исходе игры вектор выигрышей равен (-10, -8). Наконец, при согласии СССР убрать ракеты после угрозы со стороны США, несколько усиливалось военное превосходство США и причинялся сильный ущерб международному престижу СССР. Таким образом выигрыши игроков можно оценить как (1, -4).
Однако, имея такую интерпретацию развития событий, Советский Союз просто не стал бы с самого начала разворачивать ракеты на кубе, так как модель однозначно свидетельствует о выгодности выбора США в пользу угрозы и последующего выбора СССР по ликвидации базы без военного противоборства. Значит не все так просто и модель слишком грубо описывает ситуацию.
На самом деле рассматриваемый кризис конечно же не был игрой только двух лиц. И на одной, и на другой стороне на решения влияли большие команды (коалиции), причем входящие в них политики имели разные взгляды и даже самостоятельно участвовали в переговорах с лицами из другой коалиции, то есть одновременно были игроками в нескольких играх. Поэтому правильнее говорить, что существовала определенная вероятность р жесткой позиции советского руководства и вероятность (1 - р) мягкой позиции (рис. 3). Известно, например, что Кеннеди оценивал вероятность ядерного конфликта (по сути она же и вероятность жесткой позиции р) величиной в интервале от 1/3 до 0.5. При жесткой позиции СССР изменяются выигрыши в модели – проигрыш в случае вывода ракет становится сильнее, а в случае защиты ракет и ядерного противостояния – меньше («лучше смерть, чем поражение»). Для простоты на рис.3 мы просто поменяли местами выигрыши СССР, которые были при мягкой позиции в этих ситуациях. При такой структуре выигрышей Советскому Союзу уже выгоднее было защищать ракеты на Кубе в случае жесткой позиции даже несмотря на угрозу ядерной войны со стороны США.
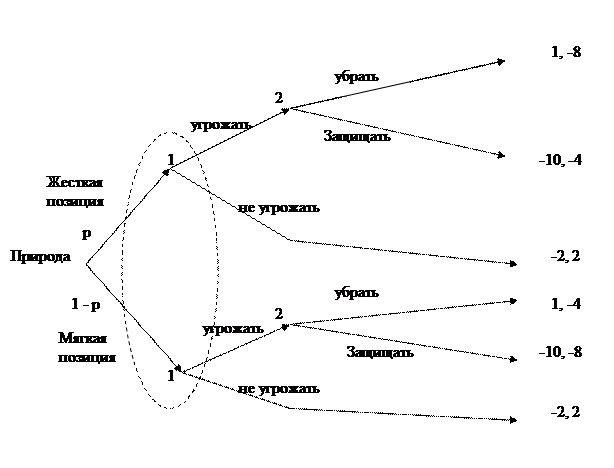
Рис. 3. Вероятностная модель Кубинского кризиса.
Оценим на основе полученной теоретико-игровой модели выигрыш США при объявлении угрозы СССР. Как видно из рис.3, в случае жесткой позиции СССР при угрозе со стороны США их проигрыш составит -10. В случае же мягкой позиции СССР выведет ракеты и тогда выигрыш США составит +1. Таким образом, в зависимости от величины вероятности р средний выигрыш США составит:
-10*р + 1*(1 – р) = 1 – 11р
При отказе США от угрозы ее выигрыш, как видно из развернутой формы игры, составит -2. Мы просто должны сравнить эти два выигрыша, потому что США стоит прибегать к угрозе в том случае, когда первый выигрыш больше второго:
1 – 11р > -2
Отсюда получается неравенство для вероятности: р < 3/11. То есть при р < 0.27 руководство США не должно угрожать СССР и смирится с размещением ракет на Кубе. Почему же тогда Кеннеди прибег к угрозе, ведь по его мнению р>1/3, то есть условие р < 0.27 не выполнялось.
Дело в том, что с такой точностью выигрыши оценить на деле не удается. А, например, при проигрыше США в случае войны величиной -100, угрожать им вообще надо только при р < 0.03. Но допустим, что выигрыши действительно такие, как показано на рис. 3. Тогда вывод такой – угрожать можно, но надо сделать проигрыш США в случае войны меньше, как бы смягчить угрозу.
2. С этой целью при моделировании конфликтов используется понятие дозированной угрозы. Уменьшение угрозы при этом достигается за счет введения вероятности реализации угрозы q. То есть угроза состоит в том, что война будет с заданной вероятностью q. Соответственно проигрыш США в случае войны будет не -10, а -10*q, то есть меньше по модулю (ведь q < 1). В случае же если войны не будет цифры проигрыша тоже поменяются – вместо -2 он составит -2*(1-q). Средний же выигрыш США в случае применения такой вероятной угрозы будет:
-10*q – 2*(1 – q) = -2 -8q
Аналогично показывается, что у СССР при жесткой позиции и защите ракет выигрыш составит:
-4*q + 2(1 – q) = 2 – 6q .
При мягкой позиции СССР и защите ракет получим:
-8q + 2(1 – q) = 2 – 10q .
Эти выражения приведены на рис.4, где теперь вместо угрозы используется термин brinkmanship, означающий в отличие от простой угрозы применение дозированной угрозы, которая реализуется с контролируемой вероятностью q. Такой подход позволяет делать важные выводы. Например, хорошо видно, что при жесткой позиции СССР защита ракет при любом q выгоднее для СССР, ведь всегда -8 < 2 – 6q. При мягкой позиции советского руководства вывод ракет будет иметь место при -4 > 2 – 10q, то есть при q > 0.6. Это условие эффективности угрозы. Оно означает, что США надо применять угрозу войны с вероятностью не менее 60%, или тогда вообще не угрожать.
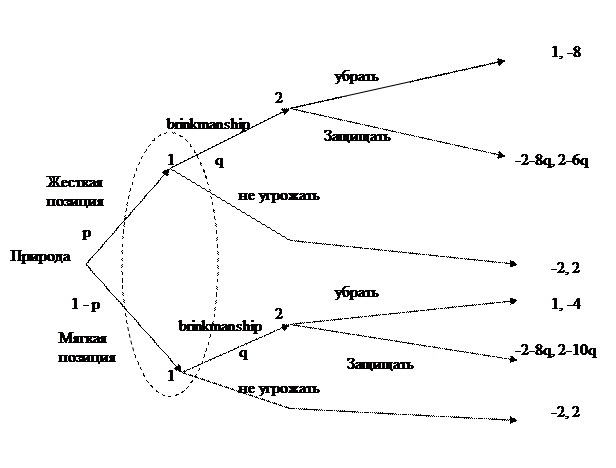
Рис. 4. Модель Кубинского кризиса с применением дозированной угрозы.
Реализация вероятной угрозы в данном случае состоит в том, что после принятия СССР решения защищать ракеты, США используют датчик случайных чисел. Например, берут случайное число с равномерным распределением в интервале (0, 1) и если оно оказывается меньше 0.6 – начинают войну. Это близко к тому, как бросают монетку, принимая ответственное решение, или крутят барабан револьвера с одним патроном, а потом стреляют («русская рулетка». В этом смысле здесь чисто случайный ход, стратегический выбор сделан раньше, в момент объявления вероятной угрозы.
Найдем приемлемый для США риск возникновения войны. Для этого вычислим средний выигрыш США при объявлении дозированной угрозы с учетом вероятностей жесткой и мягкой позиций в СССР (рис.4):
(-2 – 8q)*p + 1*(1-p) = -8pq -3p + 1
Здесь мягкая позиция соответствует выводу ракет. В случае отказа от угрозы выигрыш США составит -2. Поэтому применение угрозы выгодно для США при:
-8pq – 3p +1 > -2 .
Отсюда получаем неравенство q < 0.375(1/p – 1). Выражение q = 0.375(1/p – 1) называется условием приемлемости угрозы. Анализ соответствующей функции q(p), графиком которой является гипербола, показывает, что вероятную угрозу здесь надо применять, если р лежит в интервале (0.27, 0.38). При меньших р применима простая угроза (q = 1), а при р > 0.38 любая эффективная угроза (q > 0.6) оказывается неприемлемой для США, то есть им следует отказаться даже от вероятной угрозы (при р=0.38 функция q(p) равна 0.6 и потом убывает с ростом р).
На самом деле во время Карибского кризиса оценки вероятности р и выигрышей обоих сторон были весьма приближенными, что не позволяло рассчитать необходимую величину q и сделать вывод о целесообразности применения угрозы. Это уже потом появились мемуары и исследования, позволившие сделать приведенный выше анализ. Зато в момент самого конфликта всегда есть возможность скрининга, позволяющего опытным путем определить интересующие параметры. В случае brinkmanship эффективность заданного уровня угрозы проверяется по реакции противника. То есть если начать с малого значения q и потом постепенно его увеличивать, то при соблюдении условия приемлемости угрозы при определенном значении q вторая сторона конфликта примет ваши условия. При Карибском кризисе примерно так и было. Заявление Кеннеди о возможном объявлении морской блокады Кубы соответствует малому значению q порядка 0.02. Реальное введение блокады – это уже увеличение q. Дальнейшему увеличению q способствовала бы утечка информации о готовящемся воздушном этапе по ракетной базе. И так далее. Этот процесс нарастания угрозы продолжался до тех пор, пока СССР не принял условия США. Это оказалось возможным, потому что выполнялось неравенство р < 0.38. В противном случае угроза рано или поздно стала бы слишком опасной для США и им пришлось бы смириться с развернутой на Кубе базой СССР. Конечно, контролировать точное значение q на практике невозможно – у людей есть нервы и подчиненные не точно выполняют приказания. К тому же возможны случайные события, когда резкое увеличение q может привести к реальной войне. Поэтому такой метод выявления предела терпимости риска опасен. К тому же по мере нарастания угрозы можно потерять контроль над ситуацией и тогда даже в случае принятия ваших условий противником ситуацию не удастся ввести в мирное русло. И поняв это, противник уже не будет уступать – он скажет, что от вас уже ничего не зависит и договариваться с вами не о чем. Это ситуация, когда на ход действий влияет уже не центральная власть, а полевые командиры. Кстати во время Карибского кризиса такой эпизод тоже был, когда ВВС США провели имитацию воздушной атаки на СССР, даже не уведомив об этом президента. С точки зрения теории игр применение нарастающей угрозы в Карибском кризисе аналогично поведению игроков в игре «цыплята». И там тоже после определенного момента теряется контроль над ситуацией - столкновение машин становится неизбежным, даже если один из игроков уже решил затормозить. Можно привести и много других примеров применения стратегии brinkmanship, например, при взаимодействии Президента и парламента страны или даже в отношениях между супругами.
Вопросы:
1) Какие классические игры чаще всего используются при анализе международных отношений?
2) В чем суть игры chicken и какова ее международно-политическая интерпретация?
3) На чем основывается количественная оценка вероятности ядерного конфликта в ходе Карибского кризиса?
4) В чем недостатки классической теоретико-игровой модели Карибского кризиса?
5) Сформулируйте понятие дозированной угрозы.
6) Что обозначает термин brinkmanship?
7) Как проверяется эффективность заданного уровня угрозы?
Литература:
Учебные пособия и монографии:
1. Лефевр В.А., Смолян Г.Л. Алгебра конфликта. Изд. 2-е, стереотипное. – М.: КомКнига, 2007. – 72 с.
2. Шеллинг Т. Стратегия конфликта: Пер. с англ. – М.: ИРИСЭН, 2007. – 366 с.
3. Axelrod R. The Evolution of Cooperation. Basic Books, 2006.








