Тема: Арифметическая прогрессия

Дата: 2025-06-02; Просмотры: 19

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Цель: сегодня научимся решать задачи на нахождение элементов арифметической прогрессии.

Основные формулы

(a_n): a₁ , a₂ , a₃ , a₄ ,… , a_n-1 , a_n

(a_n) - арифметическая прогрессия, если a_{n +1} = a_n + d ,

где d-некоторое число – разность арифметической прогрессии

d = a_{n +1} - a_n - разность арифметической прогрессии

a_n+1 = a_n + d - рекуррентная формула

a_n = a ₁ + d ( n – 1) формула n -го члена арифметической прогрессии

a_n = 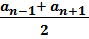- свойство арифметической прогрессии

№ 722 ( х _n ) - арифметическая прогрессия,

x₁ = 2, х ₈ = - 47

Найти: d

Решение.

Воспользуемся формулой n-ого члена a_n = a ₁ + d ( n – 1)

х ₈ = 2 + d ( 8 – 1) = - 47;

2 + 7 d = - 47;

7 d = - 47 - 2;

7 d = - 49;

d = - 49 : 7;

d = - 7.

Ответ: d = -7.

№729 ( b_n ) - арифметическая прогрессия,

b ₅ = 11, b ₁₁ = -7

Найти: b ₁

Решение.

Воспользуемся формулой n-ого члена a_n = a ₁ + d ( n – 1)

b₅ = b₁ + d( 5 – 1) = 11; b₁₁ = b₁ + d( 11 – 1) = -7;

b₁ +4 d = 11 b₁ + 10 d = -7

Решим систему уравнений: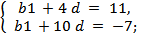

Вычтем из первого уравнения системы второе уравнение, получим: -6 d = 18.

d = 18: (-6);

d = - 3.

Подставим d = -3 в первое уравнение системы, получим b ₁ +4∙(-3) = 11.

b ₁ - 12 = 11;

b ₁ = 11 +12;

b ₁ =23.

Ответ: b ₁ =23.

№733 ( a_n ) - арифметическая прогрессия,

( a_n ) : -10,2; -9,5; -8,8; …

Найдите номер первого положительного члена

Решение.

Воспользуемся формулой n-ого члена a_n = a ₁ + d ( n – 1) и d = a_{n +1} - a_n

d= а ₂ – а ₁ = -9,5 – ( - 10,2) = - 9,5 + 10,2 = 0,7.

a_n = - 10, 2 +0,7∙( n – 1) = - 10, 2 +0,7 n – 0,7 = 0,7 n –10,9.

a_n >0, значит 0,7 n –10,9 > 0 .

0,7 n > 10,9 ;

n > 10,9 : 0,7;

n > 15 .

n – натуральное число, значит n = 16, а_{16 -} первый положительный член.

Ответ: n = 16.

Домашнее задание: сделать конспект и выполнить №№ 723,730, 734, по образцу выше( фото прислать)