Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Дата: 2025-05-01; Просмотры: 1
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

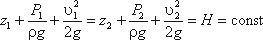
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

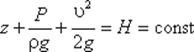
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

z1 и z2 - удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;
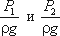- удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
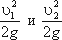- удельные кинетические энергии в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна

 
 

Уравнение Бернулли можно истолковать и геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис.2.1, можно заметить, что z1 и z2 - геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; 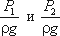- пьезометрические высоты; 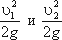- скоростные высоты в указанных сечениях.

2. Основы механики разрушения. Причины её развития и решаемые ею задачи.Основные задачи механики разрушения в рамках изучаемого курса:

– изучение условий распространения трещин в упругих и упругопластических материалах;

– решение задач распределения напряжений и деформаций в окрестностях трещин;

– введение характеристик трещиностойкости конструкционных материалов;

– изучение методов испытаний, технологических процессов и условий эксплуатации по критерию трещиностойкости;

– прогнозирование ресурса для тел с усталостными трещинами;

– прогнозирование эффективной трещиностойкости композитов.

Причинами механического разрушения элементов механических систем могут быть: трение и износ, усталость, контактные явления механической, химической и физической природы, коррозия, ухудшение эксплуатационных свойств в результате влияния различных внутренних причин и внешних воздействий. Таким образом, механическое разрушение является следствием постепенно развивающихся в механически нагруженном материале повреждений. В соответствии с этим одним из фундаментальных свойств механической прочности материалов является её зависимость от времени. Следовательно, деформация и разрушение материала характеризуются не предельными напряжениями, а скоростью деформации и разрушения или долговечностью.

В общем случае скорость процессов механического разрушения нагруженного твёрдого тела и время его разрушения зависят от структуры и свойств материала, от величины напряжения и температуры.

До недавнего времени считались общепринятыми классические представления о пластической деформации и разрушении материалов как о критических событиях, наступающих тогда, когда действующие в материале напряжения достигают некоторой критической величины. Согласно этим представлениям при напряжениях, меньших предела упругости, пластическая деформация вообще не может развиваться, а разрушение тела происходит только тогда, когда напряжения достигнут предела прочности. Однако в последнее время этому взгляду противопоставляется другой подход, согласно которому разрушение материала рассматривается не как критическое событие, а как постепенный кинетический термоактивационный процесс, развивающийся в механически напряженном материале во времени с момента приложения к нему нагрузки, в том числе меньше критической. Разрушение является безактивационным процессом лишь при очень низких температурах или при действии напряжений, равных пределу теоретической прочности.

В соответствии с этой кинетической теорией, согласно которой одним из фундаментальных свойств прочности является ее зависимость от времени, деформация и разрушение должны характеризоваться не предельным напряжением, а скоростью деформации и разрушения, а также долговечностью - временем, требующимся для разрушения. Пределы упругости, текучести, прочности являются с этой точки зрения лишь некоторыми условными характеристиками.

Скорость процессов механического разрушения нагруженного твердого тела и, соответственно, время до разрушения зависят от структуры и свойств материала тела, от напряжения, вызываемого нагрузкой, и температуры. Предложен ряд эмпирических формул, описывающих зависимость времени до разрушения от этих факторов.

 

3. Соединения пайкой и склеиванием.

При соединении пайкой в отличие от сварки место спайки на­гревается лишь до температуры плавления припоя, которая намного ниже температуры плавления материала соединяемых деталей. Соеди­нение деталей получается благодаря заполнению зазора между ними расплавленным припоем.

Припой или клей в разрезах и на ви­дах изображают линией в 2 раза толще основ­ной сплошной линии. Для обозначения пайки или склеивания применяют услов­ные знаки, которые наносят на линии-выноске от сплошной ос­новной линии. Швы, выполнен­ные пайкой или склеиванием по периметру, обозначаются лини­ей-выноской, заканчивающейся окружностью диаметром 3-4 мм.

В соединениях пайкой и склеиванием место соедине­ния элементов в разрезах и на видах показывают утолщенной контурной линией.

Если же соединяемые элементы показаны в сечении зачерненны­ми, то место соединения изображается просветом.

Обозначение соединений пайкой и склеиванием производится с помощью символов и знаков, проставляемых на линии-выноске, ко­торая заканчивается стрелкой, указывающей непосредственно шов, или точкой при указании невидимых частей соединения.

Билет 6.

1. Потери энергии при достижении жидкости:

а) по длине трубопровода;

б) местные сопротивления.

Потери напора по длине потока. Когда передвигают книгу по столу, то затрачивают энергию на преодоление силы трения о стол. При движении жидкости энергия будет затрачиваться на преодоление сил трения в жидкости. Экспериментально доказано, что при движении жидкости на стенке трубы образуется тончай­ший неподвижный слой этой жидкости. Поэтому даже на стенке трубы сохраняется жидкостное трение.

Потери напора 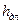на трение по длине трубы определяют по формуле

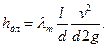
где 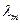— коэффициент трения; l — длина трубы; d — ее диаметр: v2/(2g) — скоростной напор.

Очевидно, что чем больше длина трубы /, тем значительнее затраты энергии на преодоление трения. И наоборот, с увеличением диаметра трубы d затраты энергии уменьшаются, так как поверхность трения становится относительно меньше.

Значения коэффициента трения 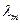, приводимые в справочни­ках, зависят от режима течения жидкости, определяемого числом Рейнольдса, а в случае развитого турбулентного течения — и от степени шероховатости трубы.

Влияние шероховатости на величину потерь напора обусловле­но образованием вихрей на выступах неровностей трубы, что тре­бует затрат некоторой доли энергии потока. Различают абсолют­ную и относительную шероховатость.