Лабораторная работа №2
«Использование t-тестов и дисперсионного анализа программы STATISTICA при сравнении исследовательских выборок статистических данных».
Цель работы.
Ознакомиться с дисперсионным анализом и использованием t-тестов программы STATISTICA. Сравнить исследовательские выборки статистических данных.
Ход работы.
1.Открыть, используя ярлык на рабочем столе программу STATISTICA на русском языке.
2. Загрузить рабочий файл «Дисперсионный анализ» со статистическими данными о параметрах эффективности или показателях работы различных категориальных групп, с единой физической основой оценок, и выбрать заданный преподавателем вариант, по которому будет проводиться анализ результатов. Обратить внимание на специфику кодировок данных для проведения t-тестов и дисперсионного анализа программы STATISTICA.
3. Используя опцию «Графика», вывести на экран общую гистограмму распределения значений показателей для всех категориальных групп, и на основе визуального анализа определить наличие (или отсутствие нескольких: двух и более) генеральных совокупностей, характерных для смешанных выборок, сравнение которых необходимо проводить с помощью дисперсионного анализа и t-тестов.
4. Из верхнего меню программы STATISTICA при помощи опции «Анализ» активировать модуль «Дисперсионный анализ - ДА» и в открывшемся окне задать параметры его работы (в данном случае «Однофакторный ДА» и «Диалог»), и после команды ОК в новом окне указать варианты зависимых переменных и категориального предиктора.
Вывести на экран полученное окно с результатами дисперсионного анализа (команды ОК последующая «Все эффекты») и зафиксировать его результаты.
SS- сумма квадратов отклонений
МС – дисперсия, MC= 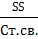
F – критерий Фишера;
P – вероятность ошибки, что данные разошлись.
5.При положительном заключении (p≤0,2) провести t-тесты, выявляющие уровни различия между парами категориальных групп по средним величинам и дисперсиям. Для этого необходимо расширить таблицу исходных данных, скопировав в новые столбики для переменных данные (наблюдения) отдельно для всех категориальных групп.
6.Активировать модуль «t-критерий для независимых переменных» при помощи опции «Анализ» головного меню, и последующей опции «Основные статистики и таблицы», и в открывшемся окне выбрать переменные для первого и второго списка. Затем активировать кнопку «Т-критерий» и зафиксировать введённую на экран таблицу с результатами статистического анализа и оценками уровней значимости расхождения и дисперсиями. При недостаточном уровне значимости (p≥0,2), прежде всего при сравнении средних, сделать заключение о принадлежности сравниваемых выборок одной генеральной совокупности, и целесообразности их объединения для получения более представительной статистики. При этом исходное количество категориальных групп будет сокращено на единицу.
Лабораторная работа №3
«Разделение смешанных одномерных статистических выборок методом подбора закона распределения в ограниченном диапазоне данных, и при помощи модуля «Кластерный анализ» программы STATISTICA».
Цель работы.
Ознакомиться с кластерным анализом в программе STATISTICA. Разделить смешанную выборку на кластеры.
Ход работы.
1.Открыть, используя ярлык на рабочем столе программу STATISTICA на русском языке.
2. Загрузить рабочий файл «Кластерный анализ» со одноимёнными статистическими данными о показателях работы групп различной генеральной совокупности, с единой физической основой оценок, и выбрать заданный преподавателем вариант, по которому будет проводиться анализ результатов.
3.Используя опцию «Графика», вывести на экран общую гистограмму смешанного распределения значений показателя для всех групп, и на основе визуального анализа определить наличие (или отсутствие) нескольких (двух и более) генеральных совокупностей, характерных для смешанных выборок, которые необходимо разделить для дальнейшего анализа. При этом, количество столбцов гистограммы целесообразно увеличить примерно вдвое (через опцию «Категории») для удобства визуального анализа.
4. Из верхнего меню программы STATISTICA при помощи опции «Анализ» активировать модуль «Кластерный анализ» (через опцию «Многомерный разведочный анализ») и в открывшемся окне задать параметры его работы (в данном случае «Кластеризация методом К-средних», ОК, «Объекты: наблюдения (строки)»); указать число кластеров (автоматически задаётся два кластера) на основе визуального анализа гистограммы для смешанной выборки или других соображений, и после команды ОК в появляющихся окнах указать опцию «Дополнительно» и «Дисперсионный анализ».
Вывести на экран полученное окно с результатами дисперсионного анализа (команда ОК) и зафиксировать его результаты.
По значению показателя p (уровня значимости, отражающего вероятность ошибочного заключения) сделать вывод о принадлежности (или её отсутствии) выделенных программой кластеров различным генеральным совокупностям.
5.При положительном заключении (p≤0,2) провести t-тесты, выявляющие уровни различия между парами категориальных групп по средним величинам и дисперсиям. Для этого необходимо расширить таблицу исходных данных, скопировав в новые столбики для переменных данные (наблюдения) отдельно для всех кластеров. Отнесение наблюдений к отдельным кластерам будет отражено в окне, открывающимся после активации опции «Сохранить классификацию и расстояние» из предыдущего окна (пункт 4 данных указаний). Более качественный анализ полученных кластеров целесообразно сделать при помощи модуля «t-критерий для независимых переменных».
6.При достаточном уровне значимости (p≤0,2) целесообразно провести визуальный анализ показателей рассеяния статистических данных для каждого кластера, путём получения гистограмм (при активации опции «Графика» головного меню), и опции «Усл. выбора». В открывшемся окне необходимо активировать опции «Использовать условия выбора» и «Заданные», после чего можно задавать верхние и нижние диапазоны данных для построения гистограмм, например: vl> x для верхнего окна (Включить наблюдения из набора переменных столбца vl со значениями величины x); vl> y для нижнего окна (Исключить наблюдения со значениями больше величины y). Получение гистограммы, хорошо согласующейся с теоретическим законом, будет свидетельствовать о качественном разделении смешанной выборки.
Вывод
Таким образом, гистограммы хорошо согласуются с теоретическим законом, свидетельствуют о качественном разделении смешанной выборки. Исходя из Рис. Визуальный анализ показателей рассеяния статистических данных для каждого кластера подтвердил соответствие выбора числа кластеров числу генеральных совокупностей с вероятностью ошибки p≤0,2.
Лабораторная работа №4
«Работа с кластерами»








