Пессимистическая позиция: - Критерий максимина (MM)
Kmm= max aim = max (min aij ). (4)
i i j
Конструктор исходит из того, что надо ориентироваться на наименее благоприятный случай и приписывает каждому из альтернативных вариантов наихудший из возможных результатов. После этого он выбирает самый выгодный вариант, т. е. ожидает наилучшего результата в наихудшем случае. Для каждого иного внешнего состояния результат может быть только равным этому или лучшим.
Позиция относительного пессимизма: - Критерий Сэвиджа
Kc = min aim = min max(max aij _– aij). (5)
i i j j
Для каждого варианта решения конструктор оценивает потери в результате по сравнению с определенным по каждому варианту наилучшим результатом, а затем из совокупности наихудших результатов выбирает наилучший согласно представленной оценочной функции.
Пусть природа находится в состоянии Qs, найдем максимальный элемент s-го столбца табл. 1.1,
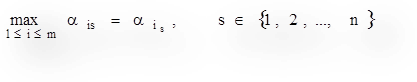 .
.
Мера сожаления определяется как разность
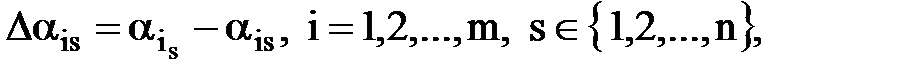
где 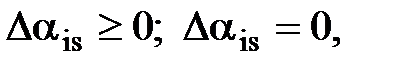 если
если 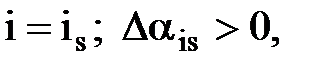 если
если 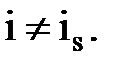 Тогда при состоянии природы Qs лучшей операцией является
Тогда при состоянии природы Qs лучшей операцией является 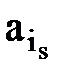 : для нее сожаление равно нулю. Изменяя последовательно значения s, s = 1,2,…, n, получим сожаление для каждой операции ai, i=1,2,…, m, при любом состояния природы Qs, s=1,2,…, n. Матрица сожалений представлена в табл. 1.2.
: для нее сожаление равно нулю. Изменяя последовательно значения s, s = 1,2,…, n, получим сожаление для каждой операции ai, i=1,2,…, m, при любом состояния природы Qs, s=1,2,…, n. Матрица сожалений представлена в табл. 1.2.
Для принятия решения к табл. 1.2 применяется критерий минимакса (minmax): для каждой операции ai, i=1,2,…, m, находится наибольшее сожаление,
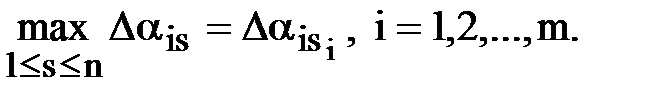
Таблица 1.2
| Qj ai | Q1 | Q2 | … | Qn |
| a1 | Da11 | Da12 | … | Da1n |
| a2 | Da21 | Da22 | … | Da2n |
| … | … | … | … | … |
| am | Dam1 | Dam2 | … | Damn |
Затем среди членов последовательности 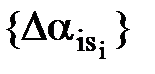 , i=1,2,…, m, s = 1,2,…, n, находится минимальный
, i=1,2,…, m, s = 1,2,…, n, находится минимальный
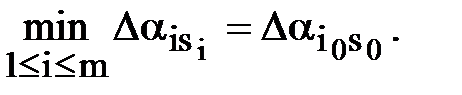
Последние два равенства соединим в одно:
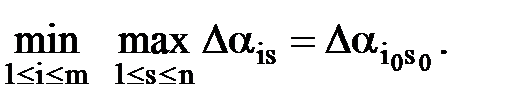 (1.7)
(1.7)
Принимаемое решение – наилучшая операция 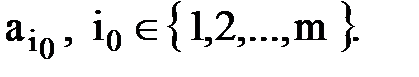
Критерий равновозможных состояний
По этому критерию выбирается та операция ai0, для которой сумма полезностей 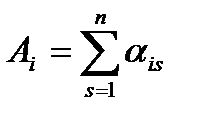 максимальна,
максимальна,
Kрс = 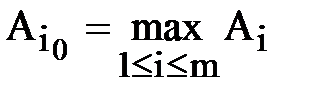 . (6)
. (6)
Принятие решений в условиях риска - Критерий Байеса-Лапласа (БЛ)
Ситуация ПР в условиях риска возникает в случаях, когда известны априорные вероятности состояний природы
р(Q1), р(Q2), … , р(Qn),
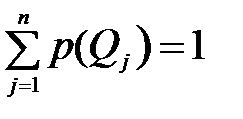 .
.
Естественно воспользоваться этой дополнительной информацией. С этой целью для каждой операции аi находят взвешенные суммы полезностей
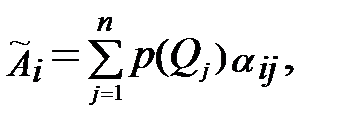 i=1,2, …, m ,
i=1,2, …, m ,
и выбирают в качестве наилучшей ту операцию 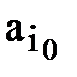 , для которой взвешенная сумма полезностей в (3.8) максимальна,
, для которой взвешенная сумма полезностей в (3.8) максимальна,
Кбл = 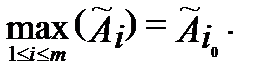 (7)
(7)
Критерий Гурвица
Стараясь занять наиболее уравновешенную позицию, Гурвиц предложил критерий (HW), оценочная функция которого находится где-то между точками зрения предельного оптимизма (2) и крайнего пессимизма (4):
Кг = max aim
i
max aim = max (cmin aij+ (1-c)max aij ), (8)
i i j j
где с — весовой множитель.
Правило выбора согласно HW-критерию формулируется нами следующим образом:
Матрица решений ||aij|| дополняется столбцом, содержащим средние взвешенные наименьшего и наибольшего результатов для каждой строки Выбираются те варианты ai0, в строках которых стоят наибольшие элементы aij этого столбца.
Для с=1 HW-критерий превращается в ММ-критерий. Для с = 0 он превращается в критерий азартного игрока. Отсюда ясно, какое значение имеет весовой множитель с. В технических приложениях правильно выбрать этот множитель бывает так же трудно,как правильно выбрать критерий. Вряд ли возможно найти количественную характеристику для тех долей оптимизма и пессимизма, которые присутствуют при принятии решения. Поэтому чаще всего весовой множитель с = 0,5 без возражений принимается в качестве некоторой «средней» точки зрения. При обосновании выбора применяют обратный порядок действий. Для приглянувшегося решения вычисляется весовой множитель с, и он интерпретируется как показатель соотношения оптимизма и пессимизма.
30 Аксиомы Эрроу
Аксиомы Эрроу
В 1951 г. Кеннет Эрроу из Стенфордского университета задался вопросом о возможности создания системы голосования, которая одновременно удовлетворяла бы трем принципам: рациональности (без противоречий, отсутствия нетранзитивности), демократичности (один человек - один голос) и разрешимости (позволяла осуществлять выбор). Такую систему он не предложил, но Эрроу разработал набор требований, аксиом, которым она должна удовлетворять. На основе приведенных аксиом Эрроу попытался в общем виде доказать существование системы голосования, удовлетворяющей одновременно трем перечисленным выше принципам. Рассмотрим эти аксиомы [3,43].
Аксиома 1 - аксиома универсальности- требует, чтобы система голосования была действенной при любом возможном распределении голосов, при любых предпочтениях избирателей.
Аксиома 2 - аксиома единогласия, в соответствии с которой единогласное мнение всех голосующих за выбор определенного кандидата должно привести к коллективному выбору этого же кандидата.
Аксиома 3 - аксиома независимости от несвязанных альтернатив - говорит о том, что в групповом упорядочении порядок определенных кандидатов не должен измениться, при изменении отношений избирателей к прочим кандидатам.
Аксиома 4 - аксиома полноты, согласно которой система голосования должна сравнивать любую пару кандидатов.
Аксиома 5 - условие транзитивности предполагает, что система голосования не должна нарушать транзитивность отношений избирателей, в ней не должно быть противоречий.
Определив пять аксиом желаемой системы голосования, Эрроу в то же время показал, что системы, удовлетворяющие этим аксиомам, обладают с точки зрения демократических свобод недопустимым недостатком: для выполнения аксиоматических требований они предполагают участие личности (диктатора), навязывающей всем остальным избирателям свои предпочтения. Требование же исключения диктатора приводит к невозможности создания системы голосования, удовлетворяющей всем аксиомам Эрроу. Поэтому результат Эрроу называют "теоремой невозможности".








